Дана матрица размерностью 5*5, заполненная случайными числами от 1 до 20. Требуется: а) определить максимальный элемент среди элементов, расположенных под побочной
диагональю матрицы;
б) составить одномерный массив из произведений каждого столбца матрицы;
в) определить № столбца, где произведение минимально.
Разрабатываемое приложение должно содержать:
1. Ввод исходных данных с датчика случайных чисел
2. Вывод на экран исходного массива
3. Необходимые вычисления
4. Вывод на экран результатов вычислений и результирующего одномерного массива
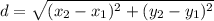
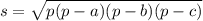, где 
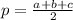-полу периметр треугольника.![\sqrt[3]{abc}](/tpl/images/0559/2002/25fb8.png)
или
2. P=a+b, S=1/2*a*b, где a и b - данные катеты
3. Пусть даны координаты трех вершин треугольника A(x1;y1), B(x2;y2), C(x3;y3).
Расстояние между двумя точками вычисляется по формуле
Тогда периметр треугольника можно вычислить по формуле:
P=sqrt((x2-x1)^2+(y2-y1)^2)+sqrt((x3-x2)^2+(y3-y2)^2)+sqrt((x3-x1)^2+(y3-y1)^2).
Площадь треугольника по формуле Герона вычисляется по формуле:
S=sqrt((sqrt((x2-x1)^2+(y2-y1)^2)+sqrt((x3-x2)^2+(y3-y2)^2)+sqrt((x3-x1)^2+(y3-y1)^2)/2*(sqrt((x2-x1)^2+(y2-y1)^2)+sqrt((x3-x2)^2+(y3-y2)^2)+sqrt((x3-x1)^2+(y3-y1)^2)/2-sqrt((x2-x1)^2+(y2-y1)^2))*(sqrt((x2-x1)^2+(y2-y1)^2)+sqrt((x3-x2)^2+(y3-y2)^2)+sqrt((x3-x1)^2+(y3-y1)^2)/2-+sqrt((x3-x2)^2+(y3-y2)^2))*(sqrt((x2-x1)^2+(y2-y1)^2)+sqrt((x3-x2)^2+(y3-y2)^2)+sqrt((x3-x1)^2+(y3-y1)^2)/2-sqrt((x3-x1)^2+(y3-y1)^2))
4. Среднее геометрическое трех чисел вычисляется по формуле
(a*b*c)^1/3