Тут четыре цикла, каждый из которых выполняет движение до конца (до тех пор, пока робот не достигнет стенки).
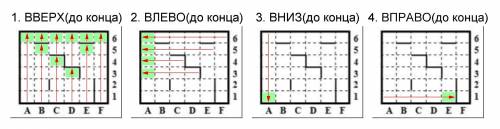
1) Нужно в уме представить клетки, в которые "упадут" роботы из всех начальных положений, если будут двигаться в первом направлении (вверх, до конца). Таких клеток окажется немного (см. рисунок 1).
2) Потом представляем, куда из этих клеток переместится робот при движении влево до конца. Таких клеток ещё меньше (см. рисунок 2).
3) Смотрим, куда попадём если вниз до конца. Останется одна клетка (см. рисунок 3).
4) И, двигаемся до конца вправо (см. рисунок 4).
Мы попадём в клетку E1.
Сюда будут попадать роботы из любого начального положения в этом лабиринте. Значит, единственная клетка, с которой робот может начать и в ней же закончить движение- это и есть клетка E1.
(см. объяснение)
Объяснение:
Пункт A:
Пусть во второй куче x камней. Тогда стратегия примет вид:
(8; x)⇒(8; 3x)
По условию 8+3x≥68 ⇒ x≥20.
Так как нам нужно найти минимальное значение, то берем число 20.
Пункт Б:
Здесь многие рекомендуют просто подбирать. Но если вы все время боитесь, что найдете подходящее значение S, а оно не окажется минимальное, попробуйте предложенный ниже вариант.
Напишем программу на языке Python 3:
def f(x, y, p):
if x + y >= 68 and p == 4:
return True
elif x + y < 68 and p < 4:
if p % 2 > 0:
return f(x + 2, y, p + 1) or f(x, y + 2, p + 1) or f(3 * x, y, p + 1) or f(x, 3 * y, p + 1)
else:
return f(x + 2, y, p + 1) and f(x, y + 2, p + 1) and f(3 * x, y, p + 1) and f(x, 3 * y, p + 1)
else:
return False
for i in range(1, 60):
if f(8, i, 1):
print(i)
Результатом ее работы будет число 19, поэтому его берем в ответ. Для самоконтроля, найденное число должно быть меньше 20, так как в противном случае Петя выиграет своим первым ходом.
Пункт В:
def f(x, y, p):
if x + y >= 68 and (p == 5 or p == 3):
return True
elif x + y < 68 and p < 5:
if p % 2 > 0:
return f(x + 2, y, p + 1) and f(x, y + 2, p + 1) and f(3 * x, y, p + 1) and f(x, 3 * y, p + 1)
else:
return f(x + 2, y, p + 1) or f(x, y + 2, p + 1) or f(3 * x, y, p + 1) or f(x, 3 * y, p + 1)
else:
return False
for i in range(1, 60):
if f(8, i, 1):
print(i)
Результатом работы программы будут два числа: 17 и 18. В ответ берем число 17.
Задание выполнено!
7
Объяснение:
В первой строке присвоить переменным a и b одинаковое значение 3
Во второй строке увеличиваем переменную a на 1, то есть а теперь равна 4 = 1 + 3 (a += 1 <=> a = a + 1)
В третьей строчке создаем переменную c и присваиваем в нее сумму а + b = 4 + 3 = 7
В четвертой строке вводим переменную с на экран