1) 0 + 1 = 1
2) 1 + 1 = 2
3) 2 + 1 = 3
4) 3 + 1 = 4
5) 4 * 2 = 8
6) 8 * 2 = 16
7) 16 + 1 = 17
8) 17 + 1 = 18
9) 18 + 1 = 19
10) 19 * 2 = 38
11) 38 * 2 = 76
12) 76 * 2 = 152
13) 152 * 2 = 304
14) 304 * 2 = 608
15) 608 + 1 = 609
16) 609 + 1 = 610
17) 610 + 1 = 611
18) 611 * 2 = 1222
19) 1222 * 2 = 2444
20) 2444 * 2 = 4888
21) 4888 + 1 = 4889
Объяснение:
Гораздо проще подобрать порядок действий, если рассматривать конечное число в двоичной системе счисления:
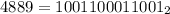
Все вычисления становятся гораздо проще и нагляднее, ведь для двоичного числа умножение на два -это просто появление справа одного нуля,
а добавление единицы -если справа (т.е. в младшем разряде) был нуль, то станет единица, а если была единица, то станет нуль, а единица перейдёт в следующий разряд (и там повторится тот же выбор).
Таким образом очень легко получить число 4889 этими действиями в двоичной системе. Получить его можно разными комбинациями указанных действий, нужно только лишь продумать действия так, чтобы их число получилось равным 21.
Вот как это выглядит, если показать результаты в двоичном виде (смотри прилагаемую картинку):
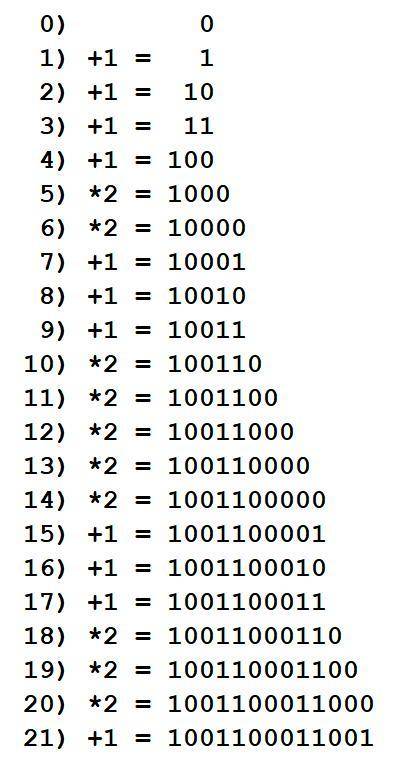
с++
#include <iostream>
#include <ctime>
using namespace std;
int main() {
srand(time(NULL));
int arr[10],sum=0;
for (int i = 0; i < 10; i++) //заполнение массива
{
arr[i] = rand() % 100;
}
for (int i = 0; i < 10; i++) //вывод массива
{
cout << arr[i] << "\t";
}
cout << endl;
for (int i = 0; i < 10; i++) //узнаем кратность чисел
{
if (arr[i] % 4 == 0) {
sum = sum + arr[i];
}
}
cout << sum << endl;
system("pause");
return 0;
}
Объяснение:
#1
sum = 0
for i in range(10):
num = int(input())
sum += num**2
print(sum)
#2
num = int(input())
lenth = len(str(num))
print(lenth)
#3
num = int(input())
sum = 0
while sum + num <= 1000:
sum += num
num = int(input())
print(sum)