
1. 1. бесконечное множество раз
2. 20
3. 11
Объяснение:
1.
M=5
Пока условие M>0 истинно выполнить M=M+5
M=5, т.е. сразу условие 5 > 0 истинно
Далее М только увеличивается (M=M+5), следовательно условие будет истинно постоянно и тело цикла выполнится бесконечное множество раз
2.
Для i от 5 до 1 выполнить
Для j от 7 до 10 выполнить
вывод строки на экран
В цикле Для переменная счётчик изменяется с шагом 1:
downto шаг -1 (минус 1)
to шаг +1 (плюс 1)
Первый цикл выполнится 5 раз (5 - 1 + 1 = 5)
Второй цикл за каждый раз выполнения первого цикла выполнится 4 раза (10 - 7 + 1 = 4)
Всего строка будет выведена на экран 20 раз (5 * 4 = 20)
3.
i=1
пока условие i<=10 истинно выполнить i=i+10 mod 3
10 mod 3 = 1 (10 - 3 * 3 = 10 - 9 = 1)
i=i+1
Т.е. за каждое выполнение цикла переменная i увеличивается на 1
Условие i<=10 будет истинно пока i изменяется от 1 до 10, как только i станет равной 11 условие будет ложным, следовательно значение i, которое выведет программа 11
mod - остаток от целочисленного деления
отметь как лучший ответ
Объяснение:
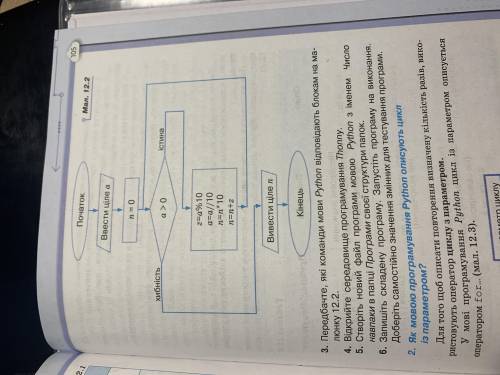
a=int(input('введите целое число:'))
n=0
if a>0:
z=a%10
a=a//10
n=n*10
n=n+z
print(n)