Объяснение:
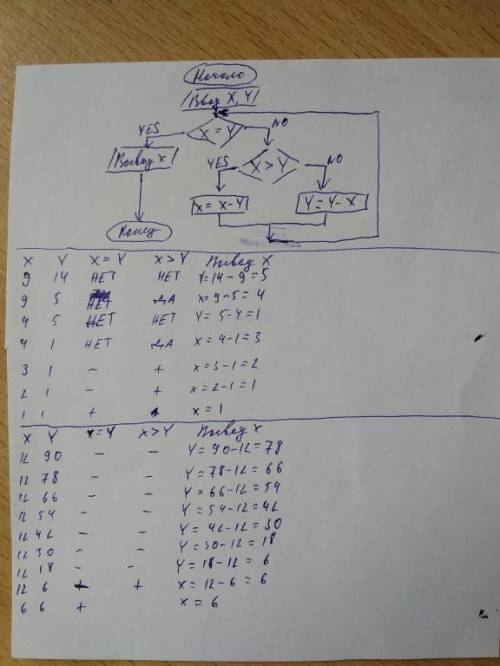
Начало;
Ввод X, Y (они у нас уже есть в табл. 1 и 2 (к примеру, в 1 табл. X=9, Y=14));
X=Y (у нас X=9, Y=14; 9 не равна 14, а это значит мы идём по стрелочке "нет");
X>Y (9 не больше 14, идём по стрелочке "нет");
Y=Y-X (подставляем в формулу наши X, Y из табл. 1 и получаем Y=14-9=5);
Теперь переходим на новую строчку табл. 1. X остаётся прежним (9), а в Y пишем тот, что мы нашли (5). Начинаем всё заново.
X=Y (9 не равна 5, идём по стрелочке "нет");
X>Y (9 больше 5, а это значит мы идём по стрелочке "да");
X=X-Y (подставляем в формулу наши X, Y. Это уже будет X=9-5=4)
Теперь переходим на новую строчку табл. 1. X теперь 4, а Y остаётся прежним (5). Начинаем всё заново.
Так проделываем каждый раз пока X не станет равно Y (в 1 табл. это 1=1).
12122
Объяснение:
Анализируем ситуацию с конца последовательности команд.
30 не является квадратом какого-либо натурального числа, поэтому последней операцией возведение в квадрат быть не может, а следовательно последняя операция - вычитание. Итак, последняя команда 2.
Рассуждаем, если в результате вычитания получили 30, то из какого числа?
x - 3 = 30
x = 33
Получается, что перед выполнением последней операции число было равным 33.
33 также не является квадратом какого-либо натурального числа, значит для его получения на предыдущем шаге была использована операция вычитания. Получается, что предпоследняя команда 2.
Из какого числа вычитали 3, чтобы получить 33?
y - 3 = 33
y = 36
Круто! 36 - это квадрат числа 6, значит была применена команда возведения в квадрат, то есть команда 1.
Так, 3 команды уже есть. Как за 2 команды из числа 3 получить число 6?
Легко! 6 = 3² - 3, т.е. была выполнена последовательность команды 1 и 2.
Всего 5 команд: 12122