7
Объяснение:
k = 1 dat[1] = 12 12 > 12 (НЕТ) m = 0
k = 2 dat[2] = 15 15 > 12 (ДА) m = 1
k = 3 dat[3] = 17 17 > 12 (ДА) m = 2
k = 4 dat[4] = 15 15 > 12 (ДА) m = 3
k = 5 dat[5] = 14 14 > 12 (ДА) m = 4
k = 6 dat[6] = 12 12 > 12 (НЕТ) m = 4
k = 7 dat[7] = 10 10 > 12 (НЕТ) m = 4
k = 8 dat[8] = 13 13 > 12 (ДА) m = 5
k = 9 dat[9] = 14 14 > 12 (ДА) m = 6
k = 10 dat[10] = 15 15 > 12 (ДА) m = 7
Не попавшую на рисунок вершину обозначим К.
С пунктом В связано наибольшее количество точек - ему соответствует П6. Пункт Е - единственный, который не связан с В - на его роль претендует только П2. Только пункт К имеет связь ровно с тремя вершинами - по таблице ему подходит П4.
Имеем:
В - П6
Е - П2
К - П4
Зная, что вершина Д связана с Е, определим по таблице, что ей подходит П7 (П4 уже занята пунктом К). Точке Г соответствует П3.
Осталось посчитать расстояния всевозможных маршрутов от В до Е и выбрать кратчайший.
В-Д = П6-П7 = 20
Д-Е = П7-П2 = 15
В-Д-Е = 20+15 = 35
В-К = П6-П4 = 25
К-Е = П4-П2 = 5
В-К-Е = 25+5 = 30
В-Г = П6-П3 = 10
Г-К = П3-П4 = 10
К-Е = П4-П2 = 5
В-Г-К-Е = 10+10+5 = 25
25 < 30 < 35
Таким образом, длина кратчайшего маршрута - 25.
Вообще, при решении подобных задач старайтесь искать какие-нибудь зацепки - например, вершины с таким количеством соседей, которого нет у других вершин (вроде вершин В и К в этой задаче). Где-то можно использовать метод исключения и т.п.
Переменную строки буду называть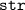 .
.
1.16.
1.17.
1.18.
Потребуется использовать