По столбчатой диаграмме видно, что русским владеют 100 человек, при этом в офисе всего 100 человек, получим что русским языком в данном офисе владеет каждый рабочий.
Так как человек 100 и процентов в одном целом тоже 100, то 1 человек будет равен 1% в круговой диаграмме.
Тогда по круговой диаграмме видно, что 70 человек владеют только одним языком, тоесть владеют только русским.
20+10=30 человек владеют 2 или 3 языками.
По столбчатой диаграмме видно, что польским владеют 30 человек. Тоесть каждый из тех, кто знает 2 или 3 языка владеет польским.
Из них 10 (данные круговой диаграммы) владеют ещё и испанским.
Тогда только польским и русским владеют 30–10=20 человек.
ответ: 20 человек.
СДНФ строится так: для каждой 1 в таблице истинности смотрим, для каких значений аргументов она получилась. Дальше для каждого набора аргументов строим конъюнкцию, в которую переменная входит как есть, если этот аргумент истинен, и отрицание аргумента, если он ложен. Все элементарные конъюнкции собираем дизъюнкциями.
1. Единицы стоят в строчках с номерами 1, 3, 4, 5, 7 (комбинации аргументов 001, 011, 100, 101 и 111). 001, например, соответствует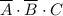 
. Итого будем иметь
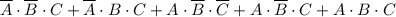
2. Аналогично, единицы для 010, 011, 100, 101:
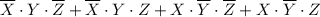
СКНФ: смотрим, где нули. Строим элементарные дизъюнкции, в которых отрицание переменной соответствует 1. Соединяем всё конъюнкциями.
1. Нули на позициях 0, 2, 6. 0=000, например, соответствует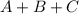 
. Получаем:
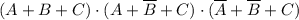
2. Аналогично, нули на позициях 000, 001, 110 и 111:
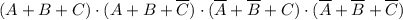
program t;
var n, i, a, b, c, d, k, m: integer; x1, x2, x3, y1, y2, y3: array[1..10000] of integer; f1, f2: text;
function icl(x, y: integer): boolean;
var i: integer;
begin
icl:=false;
for i:=1 to n do
begin
if (x>=x1[i]) and (y>=y1[i]) and (x<=x2[i]) and (y<=y2[i]) then
begin
icl:=true;
break
end
end
end;
procedure re(st, fn: integer);
var nst, nfn, i, j, jj, xx, yy: integer; eq, ff: boolean;
begin
m:=m+1;
nst:=k+1;
ff:=false;
for i:=st to fn do
begin
for j:=0 to 11 do
begin
if j mod 3=0 then continue;
xx:=x3[i]+trunc(cos(j*pi/6)*3);
yy:=y3[i]+trunc(sin(j*pi/6)*3);
if not icl(xx, yy) then continue;
eq:=false;
for jj:=1 to k do if (xx=x3[jj]) and (yy=y3[jj]) then
begin
eq:=true;
break
end;
if eq then continue;
if (xx=c) and (yy=d) then
begin
ff:=true;
break
end;
k:=k+1;
x3[k]:=xx;
y3[k]:=yy;
end;
if ff then break;
end;
if ff then exit;
nfn:=k;
if nst>nfn then
begin
m:=-1;
exit
end;
re(nst, nfn)
end;
begin
assign(f1, 'horse.in');
reset(f1);
assign(f2, 'horse.out');
rewrite(f2);
readln(f1, n);
for i:=1 to n do readln(f1, x1[i], y1[i], x2[i], y2[i]);
readln(f1, a, b);
readln(f1, c, d);
k:=1;
x3[1]:=a;
y3[1]:=b;
m:=0;
re(1, 1);
writeln(f2, m);
close(f1);
close(f2)
end.