108,16%
Пошаговое объяснение:
 , где n - кол-во периодов (год = 12 мес), r - уровень инфляции (6,3% = 0,063),
, где n - кол-во периодов (год = 12 мес), r - уровень инфляции (6,3% = 0,063), 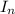 - индивидуальный индекс инфляции.
- индивидуальный индекс инфляции.
1) определяем годовой индекс инфляции:
 ≈ 2,0816
≈ 2,0816
2) определяем уровень инфляции за год:
r = (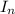 - 1) * 100% = (2,0816 - 1) * 100% = 1,0816 * 100% = 108,16%
- 1) * 100% = (2,0816 - 1) * 100% = 1,0816 * 100% = 108,16%
ответ: ожидаемый годовой уровень инфляции - 108,16%.
sin(x)+(cos(x/2)-sin(x/2))(cos(x/2)+sin(x/2))=0
1)Рассмотрим выражение под скобкой
Это разность кваратов расписанная ( х^2-y^2=(x-y)*(x+y))
Тогда свернем это,получим:
(cos(x/2)-sin(x/2))(cos(x/2)+sin(x/2))=cos^2(x/2)-sin^(x/2)
2)Видим, что это расписанная формула косинуса двойного угла, свернем это в косинус двойного угла
cos^2(x/2)-sin^(x/2)=cos(x)
3) Получили: sin(x)+(cos(x/2)-sin(x/2))(cos(x/2)+sin(x/2))=sin(x)+cos(x)=0
4)Решим полученное уравнение путем деления обеих частей на сos(x)
tg(x)+1=0
tg(x)=-1
x=-pi/4+pi*n, где n-целое число
ответ: -pi/4+pi*n, где n-целое число
Каждый месяц инфляция будет 6.3% - это значит, что цены за месяц вырастут в на 6.3%, то есть если в начале первого месяца цены были 100%, то по окончании первого месяца они будут 100% + 6.3% = 106.3%
Со вторым месяцем то же самое, только начинаем мы не со 100%, а с 106.3%. Тогда и 6.3% будут применяться уже к изначальным 106.3%, поэтому должна быть операция умножения, а не сложения.
Общая формула инфляции получается для N-го месяца при инфляции в X%: (100% + X%)^N - 100%
Минус 100%, потому что инфляция - это разность с некоторой начальной точкой, поэтому надо вычесть цены на начало первого месяца, которые мы приняли за 100%.
Не забываем, что 100% + 6.3% = 106.3% - это удобная запись в процентах, а возводить в степень надо не проценты, а само число 106.3% = 1.063
Итак, по окончании двенадцатого месяца инфляция будет (1 + 0.063)^12 - 1 = 1.08161 = 108.161%. С округлением до десятых 108.2%