Відповідь:
1) 10•10 = 100 плиток образовали бы квадрат, если бы плиток хватило. Поскольку их не хватило, то плиток меньше 100.
2) В неполном ряду плиток при раскладывании по 8 не может быть 8 (это уже полный ряд), а в неполном ряду плиток при раскладывании по 9 не может быть 0 плиток (это значит, что нет неполного ряда), а это означает, что в неполном ряду плиток при раскладывании по 8 плиток может быть только 7, а в неполном ряду плиток при раскладывании по 9 может быть только 1 плитка. Разница как раз составляет 6 плиток, как указано в условии.
3) Представим себе, что есть n полных рядов плиток при раскладывании их по 8, и есть 7 плиток в неполном ряду. Можно перекладывать из неполного ряда по одной плитке к каждому ряду, так, что в каждом ряду образуется по 9 плиток. Так можно делать до тех пор, пока в неполном ряду не останется 1 плитка:
Получаем уравнение
8n + 7 = 9n + 1
9n - 8n = 7 - 1
n = 6 рядов по 8 или по 9 плиток.
4) 8n+7 = 8•6+7=47+7=55 плиток.
Или
9n+1 = 9•6+1=54+1=55 плиток.
ответ: 55 плиток.
Покрокове пояснення:
(см. объяснение)
Пошаговое объяснение:
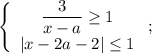
Рассмотрим сначала первое неравенство системы:
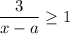
Видно, что левая его часть должна быть положительна. В свою очередь числитель дроби положителен. Это означает, что неравенство может быть верным только, если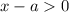 
.
Тогда при домножении левой и правой частей неравенства на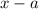 
его знак сохранится.
Получим эквивалентную систему:
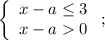
Преобразуем ее до более удобного вида:
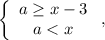
(данного результата можно было добиться также и приведением дроби к общему знаменателю; рассматриванием двух случаев; исключением одного)
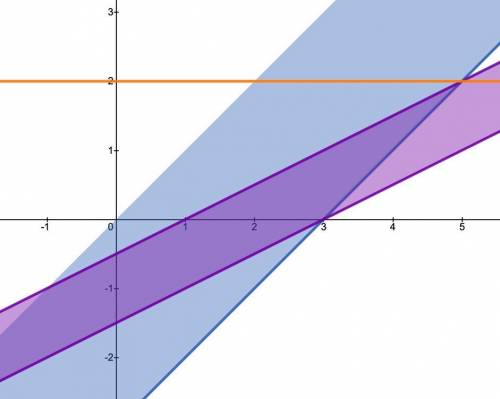
Построим решения всех неравенств записанной выше системы в координатах (x; a):
(см. прикрепленный файл | выделено синим)
Рассмотрим вторую строку системы:
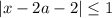
Преобразуем ее:
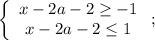
Приведем систему к более удобному виду:
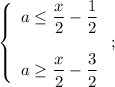
Построим решения всех неравенств записанной выше фразы в координатах (x; a):
(см. прикрепленный файл | выделено фиолетовым)
Будем двигать горизонтальную прямую до тех пор, пока не добьемся требуемого результата.
(см. прикрепленный файл | выделено оранжевым)
Тогда понятно, что достаточно решить систему:
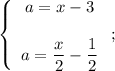
Откуда следует, что при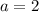 
исходная система неравенств имеет единственное решение 
.
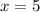Задание выполнено!
Пошаговое объяснение:
4/3+1 1/5+1 2/5=4/3+6/5+7/5=(20+18+21)/15=59/15=3 14/15 дм