ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
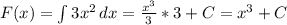
Подставляем в первообразную границы интегрирования:

2.
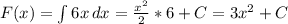
Подставляем в первообразную границы интегрирования:
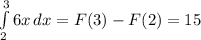
3.

Подставляем в первообразную границы интегрирования:
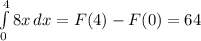
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
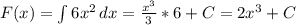
Подставляем в первообразную границы интегрирования:
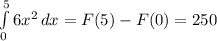
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

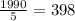
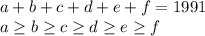 и положим что
и положим что 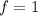 .
. 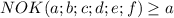
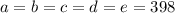 , положим что наименьшее НОК чисел есть
, положим что наименьшее НОК чисел есть 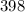 , тогда если оно будет меньше
, тогда если оно будет меньше 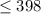 , то будет найдется такое число что
, то будет найдется такое число что 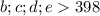 , потому что
, потому что  , и значит что НОК чисел будет уже больше
, и значит что НОК чисел будет уже больше 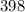
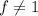 , в среднем на каждое слагаемое приходится
, в среднем на каждое слагаемое приходится 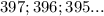 , заметим что когда
, заметим что когда 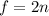 то остальные числа нечетные , когда
то остальные числа нечетные , когда 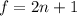 , то остальные четные , применяя такой же метод сказанный выше для
, то остальные четные , применяя такой же метод сказанный выше для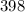
б) 24,76 кг < 2,476т
в) 20,9дм2> 0,209м2
г) 4,6 ч >270 минут