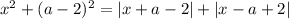
Рассмотрим правую часть уравнения.
Найдем нули модулей:
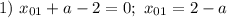
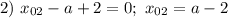
Тогда 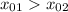 при
при 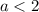 и
и 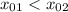 при
при 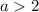 .
.
➠ Если 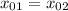 , то есть если
, то есть если 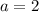 , то имеем:
, то имеем:
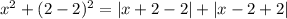
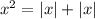
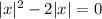
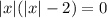
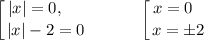
Имеем три корня. Таким образом, вариант 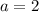 не подходит.
не подходит.
➠ Если 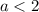 , то:
, то:
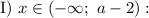
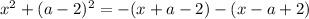
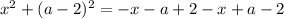
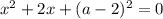
Имеем квадратное уравнение. Для того чтобы это уравнение имело один корень, нужно чтобы дискриминант данного уравнения был равен нулю:
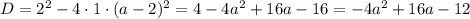
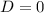 при
при 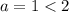 и
и 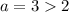
Таким образом, при 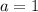 имеем решение.
имеем решение.
![\text{II}) \ x \in [a - 2; \ 2 - a]:](/tpl/images/1357/3941/2f10d.png)
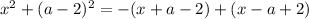
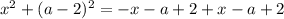
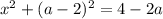
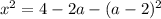
Данное квадратное уравнение будет иметь один корень, если его правая часть будет равна нулю:
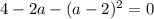
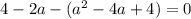
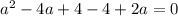
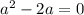
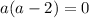
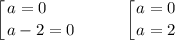
Таким образом, при 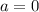 имеем единственное решение.
имеем единственное решение.
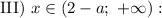
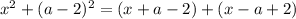
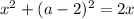
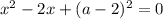
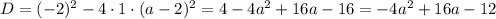
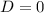 при
при 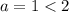 и
и 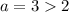
Таким образом, при 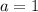 имеем решение.
имеем решение.
Следовательно, при 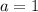 имеем два решения.
имеем два решения.
➠ Если 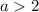 , то:
, то:
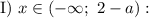
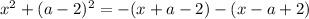
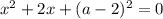
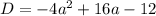
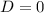 при
при 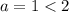 и
и 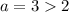
Таким образом, при 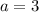 имеем решение.
имеем решение.
![\text{II}) \ x \in [2 - a; \ a - 2]:](/tpl/images/1357/3941/aa9bc.png)
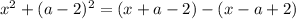
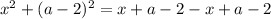
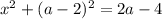
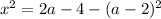
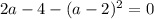
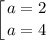
Таким образом, при 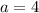 имеем единственное решение.
имеем единственное решение.
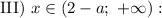
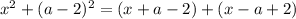
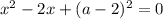
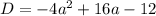
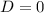 при
при 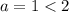 и
и 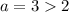
Таким образом, при 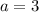 имеем решение.
имеем решение.
Следовательно, при 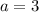 имеем два решения.
имеем два решения.
ответ: 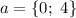

0.347648
Пошаговое объяснение:
Пусть:
1. p1 - вероятность того, что покупатель совершил покупку в первом магазине, q1=(1-p1) - вероятность того, что покупка не была совершена.
2. p2 - вероятность того, что покупатель совершил покупку во втором магазине, q2=(1-p2) - вероятность того, что покупка не была совершена.
3. p3 - вероятность того, что покупатель совершил покупку в третьем магазине, q3=(1-p3) - вероятность того, что покупка не была совершена.
Вероятность событий можно определить из выражения
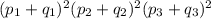
Раскрывая скобки и группируя подобные члены мы получаем вероятности событий при посещении покупателем 3 магазинов.
Интересующая нас вероятность будет равна:
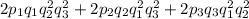
Первое слагаемое равно 0.150528
Второе слагаемое равно 0.096768
Третье слагаемое равно 0.100352
Итоговая сумма равна 0.347648
ответ: 170.
Пошаговое объяснение:
β+2β=180, β=60, искомый угол = 60+110=170.