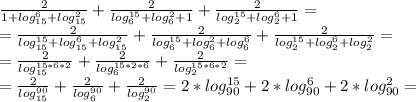Основные свои военные победы князь Александр одержал в молодости. Во время Невской битвы (1240 год) ему было от силы 20 лет, во время Ледового побоища — 22 года. Впоследствии он прославился более как политик и дипломат, однако периодически выступал и как военачальник. За всю свою жизнь князь Александр не проиграл ни одного сражения.
Александр Невский канонизирован как благоверный князь. К этому лику святых причисляются миряне, прославившиеся искренней глубокой верой и добрыми делами, а также православные правители, сумевшие в своем государственном служении и в различных политических коллизиях остаться верными Христу. Как и любой православный святой, благоверный князь — вовсе не идеальный безгрешный человек, однако это в первую очередь правитель, руководствовавшийся в своей жизни прежде всего высшими христианскими добродетелями, в том числе милосердием и человеколюбием, а не жаждой власти и не корыстью.
Основные свои военные победы князь Александр одержал в молодости. Во время Невской битвы (1240 год) ему было от силы 20 лет, во время Ледового побоища — 22 года. Впоследствии он прославился более как политик и дипломат, однако периодически выступал и как военачальник. За всю свою жизнь князь Александр не проиграл ни одного сражения.
Александр Невский канонизирован как благоверный князь. К этому лику святых причисляются миряне, прославившиеся искренней глубокой верой и добрыми делами, а также православные правители, сумевшие в своем государственном служении и в различных политических коллизиях остаться верными Христу. Как и любой православный святой, благоверный князь — вовсе не идеальный безгрешный человек, однако это в первую очередь правитель, руководствовавшийся в своей жизни прежде всего высшими христианскими добродетелями, в том числе милосердием и человеколюбием, а не жаждой власти и не корыстью.
1) 1
2) 2
Пошаговое объяснение:
1)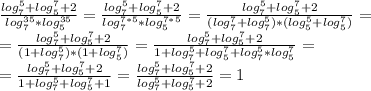
2)