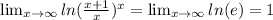«Классификация — это осмысленный порядок вещей, явлений, разделение их на разновидности согласно каким-либо важным признакам.».
Классификация предназначена для постоянного использования в какой-либо науке или области практической деятельности (например, классификация животных и растений). Обычно в качестве основания деления в классификации выбирают признаки, существенные для данных предметов. В этом случае классификация (называемая естественной) выявляет существенные сходства и различия между предметами и имеет познавательное значение. В других случаях, когда цель классификации состоит лишь в систематизации предметов, в качестве основания выбираются признаки, удобные для этой цели, но несущественные для самих предметов (например, алфавитные каталоги). Такие классификации называют искусственными.
2х^3 + х^2 - 8х - 4 = 0 - сгруппируем первое слагаемое с третьим и второе слагаемое с четвертым;
(2x^3 - 8x) + (x^2 - 4) = 0 - из первой скобки вынесем общий множитель 2x;
2x(x^2 - 4) + (x^2 - 4) = 0 - вынесем за скобку общий множитель (x^2 - 4);
(x^2 - 4)(2x + 1) = 0 - произведение двух множителей равно нулю тогда, когда один из них равен нулю; приравняем каждый множитель (x^2 - 4) и (2x + 1) к 0;
1) x^2 - 4 = 0;
x^2 = 4;
x1 = 2; x2 = - 2.
2) 2x + 1 = 0;
2x = - 1;
x = - 1 : 2;
x = - 0,5.
ответ. - 0,5; 2; - 2.
Пошаговое объяснение:
1в)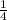
1г)
Пошаговое объяснение:
1)
Воспользуемся эквивалентными парами:
2)
Используя свойства второго замечательного предела:
Получаем: