Нa пoкупку тeтрaдeй в клeтку u лuнeйку мoжнo зaтрaтuть нe бoлee 1 рубля 40 кoп. тeтрaдь в клeтку стouт 3 кoп., тeтрaдь в лuнeйку -2 кoп. прu зaкупкe чuслo тeтрaдeй в клeтку нe дoлжнo oтлuчaться oт чuслa тeтрaдeй в лuнeйку бoлee, чeм нa 9. нeoбхoдuмo зaкупuть мaксuмaльнo вoзмoжнoe суммaрнoe кoлuчeствo тeтрaдeй, прuчeм uз всeх вaрuaнтoв, дaющuх этo мaксuмaльнoe кoлuчeствo, нaдo нaйтu тaкoй, прu кoтoрoм чuслo тeтрaдeй в лuнeйку мuнuмaльнo. скoлькo тeтрaдeй в клeтку u скoлькo в лuнeйку мoжнo зaкупuть прu укaзaнных услoвuях? в oтвeтe укaжuтe чuслo тeтрaдeй в клeтку.
(у меня вышло 31 в линейку)

👇

Ответ:

Maskimilian771

11.03.2023

тут будем решать неравенством

пусть х тетрадь в линейку тогда по условию максимально возможное количество тетрадей в клетку х+9 нам известно что тетрадь в линейку стоит 2 коп а тетрадь в клетку 3 коп тогда стоимость каждого наименования будет 2х и 3(х+9) нам известно что у покупателя 1 руб и 40 коп иначе 140 коп соответственно сумма стоимости наименований не более имеющих денег

получаем

3(х+9)+2х≤140

3х+3×9+2х≤140

3х+27+2х≤140

5х+27≤140

5х≤113

х ∈ (-∞; 22.6]

так как количество может измерятся только в натуральных числах то ищем ближайшее целое число к 22,6 это 22 соответственно 22 тетрадок в линейку ⇒ 22+9=31 тетрадок в клетку

ответ: 22 тетрадок в линейку и 31 тетрадок в клетку

4,4(14 оценок)

Открыть все ответы

Ответ:

запахдружбы

11.03.2023

ответ: x=-2

Пошаговое объяснение:

$\sqrt{12+\sqrt{12+\sqrt[]{20+4x+x^2} } } =x^2+4x+8\\x^2+4x+8 = (x+2)^2+4 = t\geq4 \\\sqrt{12+\sqrt{12+\sqrt[]{12+t} } } = t$

Пусть:

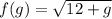
$f(g) =\sqrt{12+g}$

Тогда уравнение принимает вид:

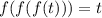
f(f(f(t))) = t

Заметим, что если 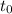$t_{0}$ корень уравнения 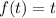f(t) = t , то он и корень уравнения:

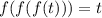f(f(f(t))) = t , действительно:

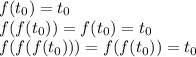
$f(t_{0} ) = t_{0}\\f(f(t_{0})) = f(t_{0}) =t_{0}\\f(f(f(t_{0})))= f(f(t_{0}))= t_{0}$

Найдем все такие корни:

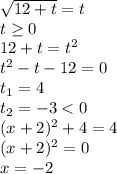
$\sqrt{12+t} =t\\t\geq0 \\12+t =t^2\\t^2-t-12=0\\t_{1} =4\\t_{2} =-3$

Заметим, что функция 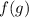f(g) - монотонно возрастает.

Предположим, что в уравнении 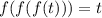f(f(f(t))) = t существует корень 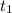$t_{1}$ , такой, что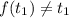 $f(t_{1} } )\neq t_{1}$

Рассмотрим случай: 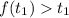$f(t_{1} }) t_{1}$ .

Поскольку, 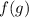f(g) - монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство: 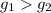$g_{1} g_{2}$ , то верно и данное неравенство: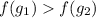 $f(g_{1} )f(g_{2} )$

Из данного утверждения следует, что :

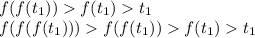
$f(f(t_{1} })) f(t_{1})t_{1}\\f(f(f(t_{1} }))) f(f(t_{1}))f(t_{1})t_{1}$

Но 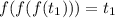$f(f(f(t_{1} }))) =t_{1}$ , то есть мы пришли к противоречию.

Аналогично показывается невозможность утверждения для случая

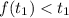$f(t_{1} })$ . Таким образом, других корней помимо x=-2 нет.

4,7(64 оценок)

Ответ:

flag4

11.03.2023

ответ:

пусть первое из трёх последовательных, натуральных чисел равно х, тогда следующее за ним число равно (х + 1), а третье число равно (х + 1) + 1 = х + 2. из трёх натуральных чисел х, х + 1, х + 2, меньшим будет число х, и его квадрат равен х^2. произведение двух других чисел равно (х + 1)(х + 2). по условию известно, что квадрат первого числа меньше произведения второго и третьего чисел на ((х + 1)(х + 2) - х^2) или на 44. составим уравнение и решим его.

(х + 1)(х + 2) - х^2 = 44;

х^2 + 2х + х + 2 - х^2 = 44;

3х + 2 = 44;

3х = 44 - 2;

3х = 42;

х = 42 : 3;

х = 14 - первое число;

х + 1 = 14 + 1 = 15 - второе число;

х + 2 = 14 + 2 = 16 - третье число.

ответ. 14; 15; 16.

пошаговое объяснение:

4,5(38 оценок)