Математика: Сумма всех целых чисел расположено между 1,8 и 3,5

Сумма всех целых чисел расположено между 1,8 и 3,5

👇

Увидеть ответ

Ответ:

GeBorgge

31.01.2020

ответ: Сумма всех целых чисел = 5

Пошаговое объяснение:

Целые числа между 1,8 и 3,5 - это 2 и 3

2+3=5

4,6(24 оценок)

Открыть все ответы

Ответ:

adidas2963

31.01.2020

№1
1. 95 * 12 = 1140 м (пройдет 1 пешеход)
2. 78 * 12 = 936 м (пройдет 2 пешеход)
3. 1140 + 936 = 2076 м = 2км 76м (расстояние между пешеходами через 12мин)
ОТВЕТ: 2км 76м
№2
1. (52 - 9*2) : 2 = 17 см (длина картона)
2. 17 * 9 = 153 см2 (площадь картона)
ОТВЕТ: 153 см2
№3
1. (4 +4) * 2 = 16см (периметр квадрата)
2. 4 * 4 = 16 см2 (площадь квадрата)
3. (24 - 2*2):2 = 10см (длина прямоугольника)
4. 10 * 2 = 20 см2 (площадь прямоугольника)
5. 24 - 16 = 8 см (периметр прямоугольника больше периметра квадрата)
6. 20 - 16 = 4 см2 (площадь прямоугольника больше площади вкадрата)
№4
1. 135 : 9 = 15м (длина зала)
2. (15 + 9) * 2 = 48м (периметр зала)
ОТВЕТ: 48м
№5
1. 360 + 365 = 725 сут
№6
1. 40 * 3 = 120 км (проехал 1 скутерист)
2. 360 - 120 = 240 км (проехал 2 скутерист)
3. 240 : 3 = 80 км/час (скорость 2 скутериста)
ОТВЕТ: 80 км/час
№7
4 пакета - 15 кг
Х пакетов - 75 кг
75 * 4 = 15 * Х
300 = 15Х
Х = 20 пакетов
ОТВЕТ: 20 пакетов
№8
1. 7 - 4 = 3м (пробежала 2 мышь)
2. 4м - 20 м/сек
    3м - Х м/сек
    20 * 3 = 4 * Х
   60 = 4Х
   Х =15 м/сек (скорость 2 мыши)
№9
1. 80 - 50 = 30 м (ширина участка)
2. (30 +80) * 2 = 220м (периметр участка)
3. 220 * 9 = 1980м = 1км 980м (потребуется проволоки)
ОТВЕТ : 1980м проповолоки

4,7(71 оценок)

Ответ:

emma66669

31.01.2020

На самом деле, числа здесь роли не играют.

Это известная комбинаторная задача. В данном случае, мы ищем максимум точек. Следовательно, по данному условию автоматически не подходят случаи с наличием пар параллельных прямых или троек (и больше) пересекающихся в одной точке прямых.

Тогда получится, что каждая прямая обязательно пересечется с каждой.

Допустим, у нас всего 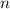прямых. Обозначим их цифрами

$1, 2, \ldots, n$

Тогда 1-я прямая имеет общие точки с прямыми 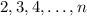$2, 3, 4, \ldots, n$ , очевидно, что таких точек (n-1)

Далее 2-я прямая имеет нерассмотренные общие точки с прямыми 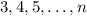$3,4,5, \ldots, n$ , их (n-2)

...

В конце концов, дойдем до последней нерассмотренной пары прямых, имеющих общую точку - прямые (n-1) и 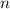, здесь всего 1 точка. А нам нужна сумма всех этих количеств, то есть

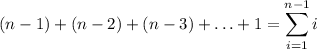
$\displaystyle (n-1)+(n-2)+(n-3)+ \ldots + 1 = \sum_{i=1}^{n-1}i$

(на последний значок можно не обращать внимание, если вам не известен, просто так красиво и правильно записывать)

На самом деле, это обычная сумма от 1 до (n-1)

В школе нередко рассказывают про Гаусса, который придумал, как быстро вычислять такие суммы (рассмотрим сначала суммы от 1 до n). Разбиваем на пары суммируемые числа, набирая с краев (так суммы будут одинаковы) и постепенно проходя к центру:

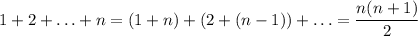
$\displaystyle 1+2+\ldots+n = (1+n)+(2+(n-1))+\ldots = \frac{n(n+1)}{2}$

Все это равно сумме первого и последнего числа, умноженной на количество таких пар (на житейском уровне это выглядит так: 1+10=2+9=...=5+6). Так как чисел 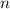, то пар в два раза меньше (пока рассматриваем четное количество чисел), вот и получили результат. Причем работает как для четного, так и для нечетного количества чисел.

Ради интереса разберу пример для нечетного количества чисел:

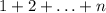
$1+2+\ldots+n$

Очевидно, что в серединке будет число, которое будет равно среднему арифметическому двух крайних чисел, слева и справа от него будет по 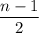$\displaystyle \frac{n-1}{2}$ чисел (например, для суммы из 11-чисел "центральным" будет 6-ое число, а слева и справа от него по 5 чисел) Добавим ему в пару такое же число и вычтем его (сумма не изменится). Тогда пар будет 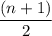$\displaystyle \frac{(n+1)}{2}$ , а сумма крайних такая же (n+1) . Следуя той же логике, получим

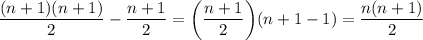
$\displaystyle \frac{(n+1)(n+1)}{2}-\frac{n+1}{2}=\bigg(\frac{n+1}{2} \bigg) (n+1-1)=\frac{n(n+1)}{2}$

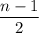Формула доказана. В нашем случае нужно её перестроить для последнего числа равного (n-1) . Сделать это несложно: сумма 1-го и последнего числа равна 1+(n-1)=n , а для подсчета количества пар условно считаем, что (n-1) - четное число (для нечетного, как мы увидели, формула та же получается), значит количество таких пар равно $\displaystyle \frac{n-1}{2}$ . Перемножаем и получаем искомую сумму 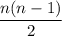$\displaystyle \frac{n(n-1)}{2}$ . Подставив вместо 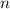значения 2,3,4,5,6 можно получать ответы на поставленные вопросы.

Если вы знаете про суммы арифметических прогрессий, тогда для 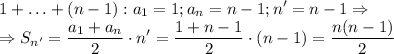$\displaystyle 1+\ldots+(n-1) : a_1=1; a_n=n-1; n'=n-1 \Rightarrow \\ \Rightarrow S_{n'}=\frac{a_1+a_n}{2}\cdot n' = \frac{1+n-1}{2}\cdot (n-1) = \frac{n(n-1)}{2}$

Та же формула.

Если вы знаете комбинаторику, то подумаем вот о чем.

Мы точно знаем, что прямая будет пересекаться с каждой прямой

Общая точка в нашем случае значит, что рассматриваются только две прямые. Тогда суммарное количество таких точек получается путем подсчета количества сочетаний (порядок не важен, 1 3 или 3 1 пересекаются) из объектов (в данном случае прямых) по 2.

Используем формулу для подсчета сочетаний.

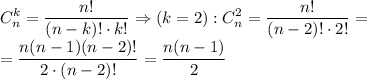
$\displaystyle C_n^k = \frac{n!}{(n-k)! \cdot k!} \Rightarrow (k=2): C_n^2 = \frac{n!}{(n-2)! \cdot 2!} = \\ = \frac{n(n-1)(n-2)!}{2\cdot (n-2)!} = \frac{n(n-1)}{2}$

Получилась та же формула.

Кстати, а возможна ли вообще такая ситуация, что прямые тройками (четверками и далее) точно не будут пересекаться друг с другом в одной точке?

Очень даже возможна. Нарисуйте окружность и постепенно проводите к ней касательные. Главное, чтобы касательные не касались окружности в одной и той же точке. Так как окружность - множество точек бесконечное по численности, то и касательных, касающиеся окружности в уникальной точке, можно провести бесконечно много (единственное, о чем надо позаботиться - чтобы не было пар параллельных друг другу касательных, но это так же возможно). Рисунок приложу

И напоследок для заданных условий посчитаем:

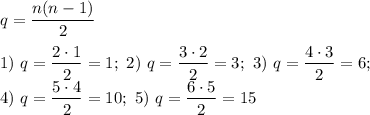
$\displaystyle q = \frac{n(n-1)}{2} \\\\ 1) \ q = \frac{2\cdot 1}{2}=1; \ 2) \ q=\frac{3\cdot 2}{2}=3; \ 3) \ q=\frac{4\cdot 3}{2}=6; \\ 4) \ q=\frac{5\cdot 4}{2}=10; \ 5) \ q= \frac{6\cdot 5}{2}=15$