в 3 номере под а):
показатели корней разные (12 и 6), мы можем получить одинаковые, умножив показатель 6 на 2, поэтому и подкоренное выражение домножаем на 2:
было: √6ой степени из 5⁵, стало: √12ой степени из 5¹⁰
то же самое в номере 3 под б):
показатели корней разные (квадратный корень из 3 и кубический корень из 9), мы можем получить одинаковые, домножив квадратный корень на 3 (чтобы получить 6) и кубический корень на 2 (чтобы получить 6), поэтому и подкоренные выражения домножаем на 2:
было: √2ой степени из 3, стало: √6ой степени из 3³ и второй множитель: было: √3ей степени из 9, стало: √6ой степени из 9²
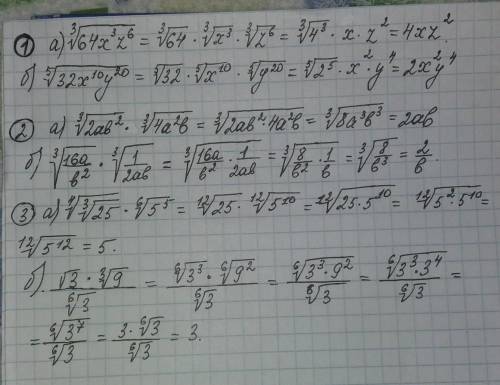
32 + (129 - х : 8) : 4 = 64
(129 - х : 8) : 4 = 64 - 32
(129 - х : 8) : 4 = 32
129 - х : 8 = 32 · 4
129 - х : 8 = 128
х : 8 = 129 - 128
х : 8 = 1
х = 1 · 8
х = 8
Проверка:
32 + (129 - 8 : 8) : 4 = 64
32 + (129 - 1) : 4 = 64
32 + 128 : 4 = 64
32 + 32 = 64
64 = 64