1) верно ли, что если каждое слагаемое делится на некоторое чис-
ло, то и сумма этих слагаемых делится на это число? проиллюстри-
руйте свой ответ примерами.
2) может ли сумма нескольких слагаемых делиться на некоторое
число, если каждое слагаемое не делится на это число? проиллюст-
рируйте свой ответ примерами.
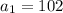
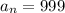
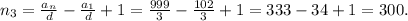
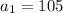

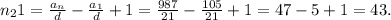
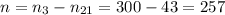 чисел.
чисел.
Пошаговое объяснение:
1. На 2 делятся все числа: В. оканчивающиеся чётной цифрой;
2. На 3 делятся все числа: Б: сумма цифр которых делится на 3;
3 На 5 делятся все числа: А: оканчивающиеся цифрами 0 и 5;
4 На 9 делятся все числа: В: сумма цифр которых делится на 9;
5 На 10 делятся все числа: Г:оканчивающиеся цифрой 0.
6 На 4 делятся все числа: Б: оканчивающиеся на две цифры, которые выражают число, которое делится на 4.;
7 Среди чисел 32 080; 1611; 3007; 91195; 1020930; 345140; 8816618 указать те, которые кратны 3: Б: 1611; 1020930;
8 Среди чисел 45678; 1300; 3456767; 7023; 40764 укажите те, которые не делятся на 2: А: 45678; 1300; 40764;
9 В школу привезли новые стулья. Мальчики перенести их в кабинеты, беря по 2 стула каждый раз. Сколько стульев могли привезти в школу? А: 108
10 Какие цифры можно подставить в число 761813* вместо *, чтобы полученное число делилось на 9? Б: 1; 10;
11 Мама купила для Васи канцелярские принадлежности. Весь товар продавец рассортировала в пакеты по 10 предметов в каждом. Может ли общее число предметов покупки быть равным? Б: 50;
12 Какие цифры можно подставить в число 601391* вместо *, чтобы полученное число делилось на 5? Б: 0; 5