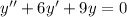
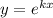 .
.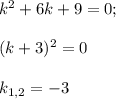
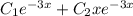
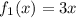 и
и 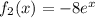
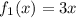
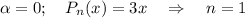
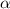 с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.
с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.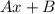
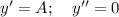 , подставим в исходное уравнение без функции
, подставим в исходное уравнение без функции 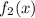 .
.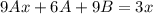
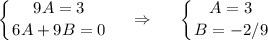
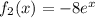
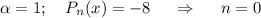
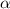 с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде:
с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде: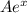
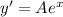 и
и 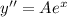
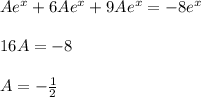
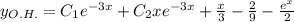
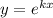 .
.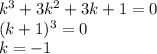
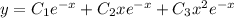
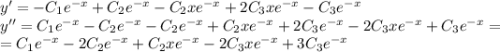
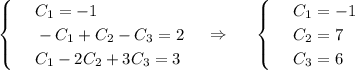
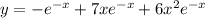
если 6 тракторов вспахивали 120 гектаров поля в день, и они вспахали поле за 4 дня, тогда площадь поля равна: 120.6.4 = 720.4 = 2880 гектаров. давайте предположим, что каждый из четырёх тракторов за 5 дней вспахал x гектаров. поэтому вся работа:
5.4.x = 20.x гектаров и все поле – 2880 гектаров
мы получаем 20x = 2880 < => x = 2880/20 = 144 гектаров в день вспахивал каждый из четырех тракторов.