Для вычисления предела на бесконечности частного двух многочленов можно сравнить степени многочленов - если степень числителя больше, то предел частного будет равен бесконечности. если степени одинаковые, то предел будет равен отношению коэффициентов при старших степенях. Если степень в значменателе больше, то предел будет равен нулю. Примеры на все три случая:
1)
2)
3)
В числителе стоит бесконечно большая функция, знаменатель стремится к 2 (то есть имеет конечный предел), значит частное будет бесконечно большим.
Наурыз - это праздник казахского народа. наурыз является новым годом в стране - казахстан, ведь весной природа начинает оживать и обретать новый прекрасный окрас. празднику наурыз уже более трех тысячи лет, этот праздник сохранился еще с тех времен, когда территорию казахстан охватили кочевые племена, населявшие всю страну. праздник наурыз казахи празднуют в марте, точнее весной. перед праздником принято отдавать долги или же продавать старые вещи. главным блюдом праздника является - наурыз коже. наурыз коже блюдо состоящее из семи ингредиентов. в ранее время, кочевники устраивали различные игры, состязания, готовили различные блюда, радуясь новому году. казахи ценят этот праздник и стараются его провести традиционно и весело.
1) -3
2) 0
3) ∞
Пошаговое объяснение:
Для вычисления предела на бесконечности частного двух многочленов можно сравнить степени многочленов - если степень числителя больше, то предел частного будет равен бесконечности. если степени одинаковые, то предел будет равен отношению коэффициентов при старших степенях. Если степень в значменателе больше, то предел будет равен нулю. Примеры на все три случая:
1)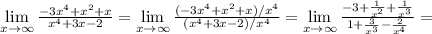
2)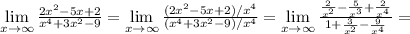
3)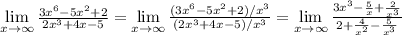
В числителе стоит бесконечно большая функция, знаменатель стремится к 2 (то есть имеет конечный предел), значит частное будет бесконечно большим.