В прямоугольном параллелепипеде все грани - прямоугольники, все рёбра равны и перпендикулярны основаниям.
Формула диагонали квадрата d=a√2 ⇒
Диагональ АС основания равна 4√2
Из прямоугольного треугольника АА1С по т.Пифагора боковое ребро
АА1=√(А1С²-AC²)=√(81-32)=7 (ед. длины)
-------
Вариант решения.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Измерениями прямоугольного параллелепипеда являются длины трех ребер, исходящих из одной его вершины. Отсюда следует:
D²=a²+b²+c², где а и b- стороны основания, с - боковое ребро.
По условию а=b=4. D=9
81=16+16+c² ⇒
c²=81-32=49
c=7 - длина бокового ребра.

x∈ (-n-2;-n+2]
Пошаговое объяснение:
Вычислим радиус сходимости:
Находим область сходимости степенного ряда:
x∈(-n-2; -n+2)
Остаётся проверить сходимость ряда на концах данного интервала.
При х = -n-2 мы получим следующий ряд:
∑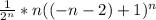 =∑
=∑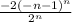
Рассмотрим первых 3 члена данного ряда: -2; 1/8; -128
Данный ряд будем исследовать по признакам Лейбница
Как видим, выполняется лишь второе условие Лейбница, а значит ряд расходится => x=-n-2 является точкой расходимости.
Рассматриваем второй конец x=-n+2
Получаем следующий ряд
∑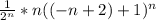 =∑
=∑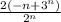
Тут исследуем по признакам Даламбера
q=1 - неопределённость, т.к. при q>1 ряд расходится, а при q<1 - сходится.
q<1 , а это значит, что ряд сходится. х=-n+2 является точкой сходимости.
Тогда данный степенной ряд является сходящимся при x∈ (-n-2;-n+2]