(x²-10x+25)-2x+10+(x²+10x+25)
x²-10x+25-2x+10+x²+10x+25
2x²-2x+60=0 |:2
x²-x+30=0
(1/5)²-1/5+30=0
1/25-1/5+30=0 |×25
1-5+75=71
80 дет./мин.
Пошаговое объяснение:
Сначала I и II станок работали одновременно 1 ч. Производительность у них была одинаковая: 70 деталей/мин.
Значит за 1 час (т.е. за 60 мин.) на этих станках сделали по 70·60=4200 (деталей).
По истечении 1 часа включается в работу III станок, производительность которого неизвестна.
I станок снижает свою производительность на 10дет/мин: 70-10=60(дет/мин).
У II станка производительность остается 70дет/мин.
Время, которое работали три станка одновременно, неизвестно, обозначим его через х мин.
За х мин. на III станке было сделано столько деталей, сколько было к этому моменту на I станке:
60х - количество деталей, сделанных на I станке за х мин.
4200 - количество деталей, сделанных на I станке за первый час работы.
Всего на I станке сделано: 60х+4200 (деталей).
После этого станки работают ещё 3,5 часа, т.е. 210 минут.
Получается, что одновременно три станка работает х+210 минут.
За это время на III станке сделано столько деталей, сколько и на втором:
70(х+210) - количество деталей, сделанных на II станке за (х+210) мин.
4200 - количество деталей, сделанных на II станке за первый час работы.
Всего на II станке сделано: 70(х+210)+4200 (деталей).
Тогда производительность III станка можно записать как
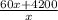
или
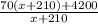
Эти две величины одинаковые. Приравниваем их и решаем получившееся уравнение.
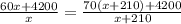
По свойству пропорции:

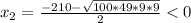 - не имеет физического смысла.
- не имеет физического смысла.
Значит три станка одновременно работали 210 мин.
В выражение
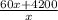
подставляем х=210 и находим производительность III станка.

ответ: производительность III станка 80 дет/мин.
80 дет./мин.
Пошаговое объяснение:
Сначала I и II станок работали одновременно 1 ч. Производительность у них была одинаковая: 70 деталей/мин.
Значит за 1 час (т.е. за 60 мин.) на этих станках сделали по 70·60=4200 (деталей).
По истечении 1 часа включается в работу III станок, производительность которого неизвестна.
I станок снижает свою производительность на 10дет/мин: 70-10=60(дет/мин).
У II станка производительность остается 70дет/мин.
Время, которое работали три станка одновременно, неизвестно, обозначим его через х мин.
За х мин. на III станке было сделано столько деталей, сколько было к этому моменту на I станке:
60х - количество деталей, сделанных на I станке за х мин.
4200 - количество деталей, сделанных на I станке за первый час работы.
Всего на I станке сделано: 60х+4200 (деталей).
После этого станки работают ещё 3,5 часа, т.е. 210 минут.
Получается, что одновременно три станка работает х+210 минут.
За это время на III станке сделано столько деталей, сколько и на втором:
70(х+210) - количество деталей, сделанных на II станке за (х+210) мин.
4200 - количество деталей, сделанных на II станке за первый час работы.
Всего на II станке сделано: 70(х+210)+4200 (деталей).
Тогда производительность III станка можно записать как
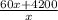
или
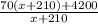
Эти две величины одинаковые. Приравниваем их и решаем получившееся уравнение.
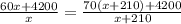
По свойству пропорции:

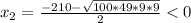 - не имеет физического смысла.
- не имеет физического смысла.
Значит три станка одновременно работали 210 мин.
В выражение
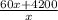
подставляем х=210 и находим производительность III станка.

ответ: производительность III станка 80 дет/мин.
ответ:45
Пошаговое объяснение:
(x-5)^2-2(x-5)+(x+5)^2=x^2-10x+25-2x+10+x^2+10x+25=2x^2-2x+60=2(x^2-x+30)
2(1.5^2-1.5+30)=2(2.25-1.5+30)=2(0.75+30)=2*22.5=45