0.7
Пошаговое объяснение:
всего в коробке 7+3=10 шаров
вероятность вынуть первый белый шар равна 7/10
вероятность вынуть первый черный шар равна 3/10
А теперь смотрим, если первым вытянули белый шар, то в коробке осталось 6 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 6/9=2/3.
Если первым вытянули черный шар, то в коробке осталось 7 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 7/9
Задача на полную вероятность:
Гипотезы:
B - первым вынули белый шар.
C - первым вынули черный шар.
P(B)=7/10
P(C)=3/10
A-вторым вынули белый шар.
Условные вероятности:
A/B - вторым вынули белый шар, при условии что первым вынули белый шар.
A/C-вторым вынули белый шар, при условии что первым вынули черный шар.
P(A/B)=2/3
P(A/C)=7/9
Формула полной вероятности:
P(A)=P(B)*P(A/B)+P(C)*P(A/C)
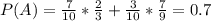
0.7
Пошаговое объяснение:
всего в коробке 7+3=10 шаров
вероятность вынуть первый белый шар равна 7/10
вероятность вынуть первый черный шар равна 3/10
А теперь смотрим, если первым вытянули белый шар, то в коробке осталось 6 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 6/9=2/3.
Если первым вытянули черный шар, то в коробке осталось 7 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 7/9
Задача на полную вероятность:
Гипотезы:
B - первым вынули белый шар.
C - первым вынули черный шар.
P(B)=7/10
P(C)=3/10
A-вторым вынули белый шар.
Условные вероятности:
A/B - вторым вынули белый шар, при условии что первым вынули белый шар.
A/C-вторым вынули белый шар, при условии что первым вынули черный шар.
P(A/B)=2/3
P(A/C)=7/9
Формула полной вероятности:
P(A)=P(B)*P(A/B)+P(C)*P(A/C)
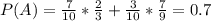
Как быстро посчитать сумму всех чисел от 1 до 100?
Сгруппируем слагаемые следующим образом:
(1 + 100) + (2 + 99) + ... + (49 + 52) + (50 + 51)
Каждая из сумм в скобках равна 101, а всего таких скобок 50. Значит, сумма всех чисел от 1 до 100 равна
101 × 50 = 5050
Аналогичным образом доказывается общая формула для суммы всех чисел от 1 до n, где n — произвольное целое число:
1 + 2 + ... + (n – 1) + n = n × (n+1) / 2
Примечание: В качестве иллюстрации к этой головоломке приведён портрет великого немецкого математика Карла Фридриха Гаусса. Согласно легенде, когда учитель математики задал маленькому Гауссу точно такую же задачу с целью надолго его занять, тот практически мгновенно решил её в уме, причём именно таким как описано выше.