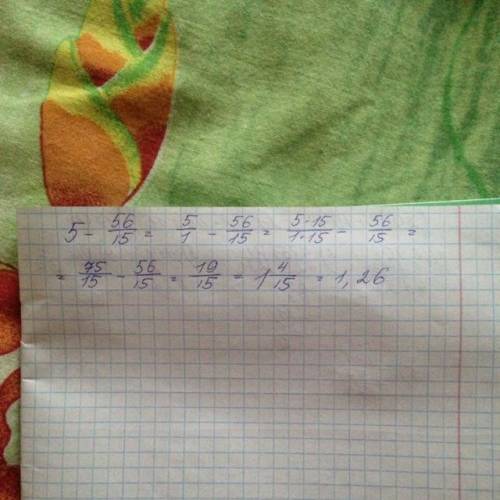
. Условие, что выражение равно единице, можно записать так:
(100 + n)k(100 - n)l = 100k + l. Так как правая часть четна, то и левая часть должна быть четна, значит, n четно. Аналогично, левая часть делится на 5, значит, n делится на 5. Значит, n делится на 10. Можно перебрать все 9 возможных вариантов: n = 10, 20, ..., 90. Например, если n = 10, то левая часть делится на 11, что невозможно.Можно обойтись без перебора: пусть n не делится на 25. Тогда числа 100 - n и 100 + n тоже не делятся на 25. Значит, пятерка входит в разложение левой части на простые множители ровно k + l раз. Но она входит в разложение правой части 2(k + l ) раз -- противоречие. Итак, n делится на 25. Аналогично доказывается, что n делится на 4. Но тогда n делится на 100, что невозможно, ибо 0 < n < 100.
5 - это
Сначала нужно найти общий знаменатель (найти наименьшее общее кратное 1 и 15 (сейчас это 15)), затем, разделить каждый общий знаменатель на знаменатели дробей и не это число умножить числитель. (общий знаменатель - 15. заменитель первой дроби - 1. 15 ÷ 1 = 15. это значит, что числитель первой дроби нужно умножить на 15). тоже самое делаем с второй дробью. (Я записываю дополнительный множитель в скобках вплотную к числу).
Затем, домножив числители выполняем действие (В знаменателе у нас общий знаменатель).
Сокращаем: просто ищем число, на которое можно одновременно разделить оба числа, чтобы получить другие целые числа. (сейчас я выбрал 3)
Теперь будет проще перевести дробь в десятичную. Дробь - это деление числителя на знаменатель, поэтому её можно записать, как:
3 ÷ 5 = 0.6
ответ: 0.6