Математика: Скалярное произведение векторов хелп

Скалярное произведение векторов хелп

👇

Открыть все ответы

Ответ:

akvilon76

06.11.2021

Диагональ делит трапецию на два треугольника. Средняя линия трапеции является также и средней линией обоих треугольников. Следовательно, основания треугольников (они же и основания трапеции) равны
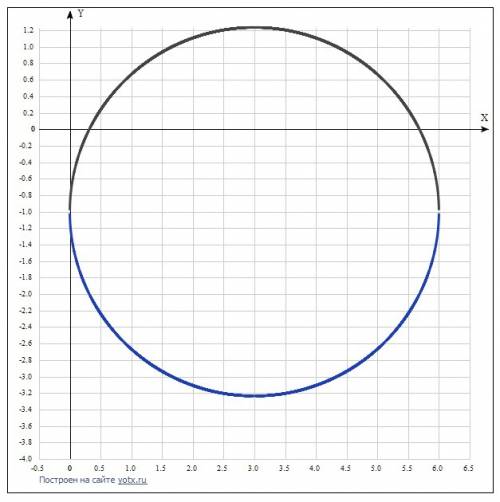
a = 15*2 = 30 см; b = 28*2 = 56 см.

Если опустить две высоты из концов меньшего основания а= 30 см на основание b = 56 см, то получится посередине прямоугольник, по бокам 2 равных прямоугольных треугольника. Горизонтальный катет каждого треугольника равен (56 - 30):2 = 13 см. Гипотенуза - боковая сторона трапеции - 26 см.
Острый угол трапеции можно найти по соотношению сторон прямоугольного треугольника:
$cos \alpha = \frac{13}{26} = \frac{1}{2}$

Острый угол трапеции равен 60°,
тупой угол трапеции равен 180°- 60°=120°

4,4(96 оценок)

Ответ:

kaliyeva2006amina

06.11.2021

Уравнение заданного эллипса как уравнение линии второго порядка имеет вид: 5x²+9у²-30x+18y+9 = 0.
Чтобы найти ответы к заданию: "Найти полуоси фокусы, эксцентриситет эллипса", надо привести уравнение к каноническому виду.
Выделяем полные квадраты.
5(x²-6х +9)+9(у²+2у+1)-45 = 0.
5(х-3)²+9(y+1)²-45 = 0.
Перенесём свободный член направо и разделим обе части уравнение на него.
Получаем каноническое уравнение эллипса.
((x-3)²/9) + ((y+1)²/5) = 1 или
((x-3)²/3²) + ((y+1)²/(√5)²) = 1.
По этому уравнению находим значения полуосей:
а = 3,
в = √5.
Центр эллипса находится в точке О(хо; уо) = О(3; -1).
Вершины эллипса имеют координаты:
А1 = ((а + хо); уо) = (3 + 3 = 6, -1) = (6; -1).
А2 = ((-а + хо); уо) = (-3 + 3 = 0, -1) = (0; -1).
В1= (хо; (в + уо)) = (3; (√5 +(-1)) =(3; (√5 - 1).
В2 = (хо; (-в + уо)) = (3; (-√5 - 1)) = (3; (-√5 - 1).
Половина межфокусного расстояния с = √(а² - в²) = √(9 - 5) = √4 = 2.
Координаты фокусов:
F1 = (с +хо); уо) = (2 + 3 = 5; -1) = (5; -1),
F2 = (-c + xo; yo) = (-2 + 3 = 1; -1) = (1; -1).

Эксцентриситетом эллипса называют отношение ε = c/a , которое может принимать значения в пределах 0 ≤ x < 1.

В нашем случае: ε = 2/3.

Для построения графика удобнее преобразовать уравнение относительно у:

(y+1)²/(√5)² = 1 - ((x-3)²/3²),

(y+1)² = 5 - 5√(1 - ((x-3)²/3²)),

у = +-(√5 - 5((x-3)²/3²)) - 1.

Уравнение с плюсом определяет верхнюю дугу эллипса, с минусом

– нижнюю дугу эллипса.
Найти полуоси фокусы, эксцентритет эллипса: 5x^2+9у^2-30x+18y+9