Решим задачу.
1. нам нужно узнать на сколько больше километров проехал второй автомобиль, чем первый.
9-4=5 километров
2. Теперь мы можем узнать сколько грамм бензина расходуется на один километр пути.
600/5=120 грамм бензина
3. Узнаем сколько грамм бензина израсходовал первый автомобиль.
4*120=480 грамм бензина
4. Узнаем какое количество граммов бензина израсходовал второй автомобиль.
9*120=1080 грамм бензина
ответ: Первый автомобиль израсходовал четыреста восемьдесят грамм бензина, второй автомобиль израсходовал одну тысячу восемьдесят грамм бензина.
ответ: 60° .
Пошаговое объяснение:
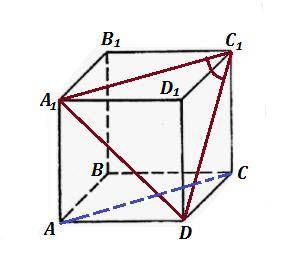
У куба все грани - это квадраты с одинаковыми сторонами . Значит диагонали граней - это диагонали равных квадратов, они равны между собой .
Диагональ А₁С₁ параллельна диагонали АС . Значит, можно рассматривать не угол между АС₁ и С₁D , а угол между А₁С₁ и С₁D .
Если достроить треугольник А₁С₁D , то он будет равносторонним, так как диагональ А₁D равна диагоналям А₁С₁ и С₁D . А все углы в равностороннем треугольнике равны 60° .
Значит, ∠А₁С₁D=60° . И угол между АС и С₁D тоже равен 60° .
Если a - направляющий вектор первой прямой, а b - направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b|/ |a| · |b|.
Если дано каноническое уравнение прямой
( x - x0)/ l = (y - y0)/ m = (z - z0)/ n, то направляющий вектор имеет вид {l; m; n}.
Находим вектор АВ по точкам А (-2,-3,1) и В (1,1,1).
АВ = (1-(-2)=3; 1-(-3)=4; 1-1=0) = (3; 4; 0).
У первой прямой направляющий вектор дан в уравнении:
n = (-2; -1; 3).
ответ: cos α = |3*(-2)+4*(-1)+0*3|/(√(9 + 16 + 0)*√(4 + 1 + 9)) =
= |-6 - 4 + 0|/5√14 = 10/5√14 = 2/√14 = 2√14/14 = √14/7.
α = arc cos(√14/7) = arc cos 0,5345 = 1,00685 радиан или 57,6885°.
Примечание. прямая в пространстве может быть в виде общих уравнений двух пересекающихся плоскостей.
Для решения данной задачи нужны направляющие векторы прямых.