Пошаговое объяснение:
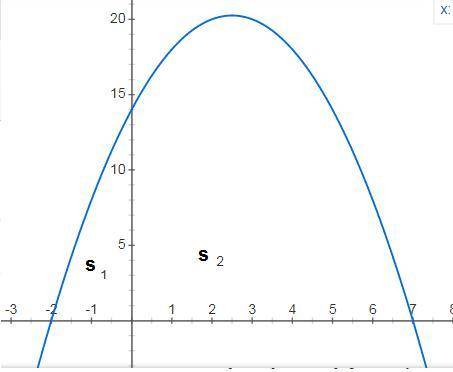
найдем точки пересечения с ОХ
5x+14-x²=0; умножим на -1 ; x²-5x-14=0 ; x₁₋₂=(5±√(25+56)/2=(5±√81)/2=
=(5±9)/2={-2;7}
найдем отдельно площади для х≤0 х≥0 и сложим
₀ ₀
S₁=-∫(5x+14-x^2)dx=-[(5x²/2)+14x-(x³/3)]=-[(5*4/2)-14*2+8/3]=
⁻² ⁻²
=-[10-28+(8/3)]=18-2 2/3=16-2/3=15 1/3
₇ ₇
S₁=∫(5x+14-x^2)dx=[(5x²/2)+14x-(x³/3)]=
⁰ ⁰
=-[(5*49/2)+14*7-342/3]=122,5+98-114=106,5=106 1/2
S=S₁+S₂=15 1/3+106 1/2=121 5/6 кв. единиц
Пошаговое объяснение:Запишем уравнения касательной в общем виде:
yk = y0 + y'(x0)(x - x0)
По условию задачи x0 = 1, тогда y0 =1²+3= 4
Теперь найдем производную:
y' = (x²+3)' = 2*x
следовательно:
f'(1) = 2·1 = 2
В результате имеем:
yk = y0 + y'(x0)(x - x0)
yk=4+2·(x-1)
или
yk = 2·x+2
Итак, уравнение касательной у= 2х+2
Для построения касательной (прямой) зададим 2 точки ,
х -1 2
у 0 6
т.е (-1; 0) и (2; 6) и проведём через неё прямую(касательную)
Для построения графика функции у=х²+3 (параболы)зададим несколько точек:
х -2 -1 0 1 2
у 7 4 3 4 7 и проведём через них параболу
Пошаговое объяснение: