Question

Есть квадрат 1 на 1,
его поделили на n треугольников - именно треугольников.
и доказать, что есть треугольник, которым можно покрыть квадрат (1/ n) x (1/n)

Answer 1

Заметим, что у любого треугольника внутри квадрата со стороной 1 периметр не может превышать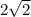 $2\sqrt{2}$. По принципу Дирихле, у нас найдется треугольник площадь которого не меньше 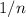$1/n$. Тогда радиус вписанной окружности для этого треугольника

$r=\frac{S}{p} \ge \frac{1/n}{\sqrt{2}}$

А это значит, что в него можно вписать квадрат со стороной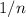 $1/n$, что и требуется.