9 монет за 1 взвешивания
Пошаговое объяснение:
27:3=9 в какой то стопки фильшивая потому две стопки будут весить одиново а третья легче
Благодаря известной точке М(2,5) мы можем найти значение b в уравнении параболы. Подставим 2 вместо Х и 5 вместо У в уравнение параболы (числа взяты из координат точки М):
5 = –2² + 2b + 5
–4 + 2b = 0
2b = 4
b = 2
Отсюда уравнение параболы имеет вид:
у = –х² + 2х + 5
При х² у нас отрицательное число (–1), значит, ветви параболы направлены вниз. Вершина параболы – её точка максимума, т.е. наибольшее значение, которого она достигает по оси ОУ (ось ординат).
Координаты вершины можно найти двумя . Приведём оба.
1. Напрямую через формулу.
Формула координаты Х вершины параболы:
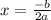
У нас –b = –2, a = –1, отсюда:
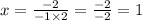
Координату У вершины параболы можно найти подстановкой в формулу параболы (х=1):
у = –1² + 2×1 + 5 = –1 + 2 + 5 = 6.
Отсюда координаты вершины параболы: (1, 6).
2. Через производную
Если Вы умеете находить производную, то этот тоже подойдёт: минимум/максимум функции находятся при приравнивании первой производной к нулю.
у = –х² + 2х + 5
Первая производная:
у' = –2х + 2
Приравниваем к нулю:
–2х + 2 = 0
2х = 2
х = 1
Далее, аналогично первому , просто подставляем х=1 в формулу параболы:
у = –1² + 2×1 + 5 = –1 + 2 + 5 = 6.
Отсюда координаты вершины параболы: (1, 6).
ответ: (1, 6).
Пошаговое объяснение: разделяете 27 монет на три столбика по 9 монет. взвешиваете два из них. Если равновесие - фальшивка в третьей стопке. Если нет - в той стопке, которая легче. имеем 9 монет, среди которых фальшивка. Опять делим на три стопки по 3 монеты. Взвешиваем два из них. Если равны - фальшивка в третьей стопке, если нет - в той что легче. У нас осталось три монеты. Взвешиваем две из них. Если их вес одинаков, то фальшивка - третья монета. Если нет - та что легче.