ответ: Ошибся
Предположим, что Миша не ошибся, так как все остатки получились разными(у девятизначаного числа при делении на каждую из его цифр 9 разных остатков), значит все цифры его различны, а так как по условию не было нулевых цифр, то наше число это какая-то перестановка чисел от 1 до 9.
Рассмотрим признаки делимости на 3 и на 9 :
Число делится на 3 или 9 если сумма его цифр делится на 3 или 9 соответственно
Так как мы знаем все цифры числа можем посчитать его сумму: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
Так как 45 делится на и на 9 и на 3 без остатка, то при делении на 3 и на 9 наше число дает одинаковый остаток, равный нулю. Также при делении на 1, очевидно, наше число даст остаток 0. Получаем, что минимум 3 остатка одинаковые, а значит, даже если при делении на остальные цифры, число даст разные остатки, то все равно мы получим максимум 7 разных остатков. Противоречие, следовательно, Миша ошибся
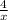 =
= 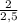
3/5 = 6/10 = 0,6 - доп. множ. 2
1/4 = 25/100 = 0,25 - доп. множ. 25
13/20 = 65/100 = 0,65 - доп. множ. 5
3/25 = 12/100 = 0,12 - доп. множ. 4
19/40 = 475/1000 = 0,475 - доп. множ. 25
103/125 = 824/1000 = 0,824 - доп. множ. 8
7/250 = 28/1000 = 0,028 - доп. множ. 4
492/500 = 984/1000 = 0,984 - доп. множ. 2
83/400 = 2075/10000 = 0,2075 - доп. множ. 25
1231/2500 = 4924/10000 = 0,4924 - доп. множ. 4
Можно сделать проще: разделить числитель на знаменатель
3/25 = 3 : 25 = 0,12
19/40 = 19 : 40 = 0,475
1231/2500 = 1231 : 2500 = 0,4924
и т.п.