Question

Докажите, что в плоском графе найдётся вершина, из

которой выходит не более 5 рёбер.​

Answer 1

Предположим обратное: у всех плоских графов степень вершин не меньше 6. Тогда, по лемме о рукопожатиях,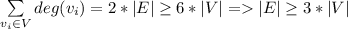 $\sum\limits_{v_i\in V} deg(v_i)=2*|E|\geq 6*|V|=|E|\geq 3*|V|$

С другой стороны, для любого плоского графа справедливо неравенство $|E| \leq 3*|V|-6$

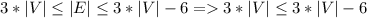Тогда $3*|V|\leq |E| \leq 3*|V|-6=3*|V|\leq 3*|V|-6$ - противоречие.

А значит предположение неверно.

А значит в любом плоском графе найдется вершина, степень которой не превосходит 5.

Ч.т.д.

___________________________

$E$ - мн-во ребер графа, $V$ - мн-во вершин, $|A|$ - мощность мн-ва $A$ (т.е. кол-во элементов этого множества), $deg(v)$ - степень вершины $v$

___________________________

Док-во неравенства $|E| \leq 3*|V|-6$

Обозначим через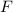 $F$ множество граней связного плоского графа.

Очевидно, что каждая грань задается не менее чем двумя ребрами. При этом каждое ребро входит не более чем в 2 грани. Тогда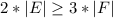 $2*|E|\geq 3*|F|$

По формуле Эйлера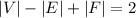 $|V|-|E|+|F| = 2$, тогда, подставив полученное неравенство, имеем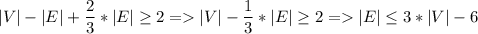 $|V|-|E|+\dfrac{2}{3}*|E| \geq 2=|V|-\dfrac{1}{3}*|E| \geq 2=|E|\leq 3*|V|-6$

В случае несвязного графа выделим в нем компоненты связности, и к каждой из них применим вышеприведенные рассуждения. Сложив полученные неравенства, получим искомое неравенство

Ч.т.д.

Answer 2

Предположим обратное: из каждой вершины выходит по крайней мере 6 ребер. Тогда достаточно доказать, что эйлерова х-ка не равна 2. То есть не выполняется равенство $V-E+F=2$;

Итак, из каждого ребра выходит по крайней мере 6 ребер. Значит, всего ребер не менее, чем $6V/2=3V$; $E\geq 3V$

Пусть $a_{i},\; 1\leq i\leq F$ - количество ребер i-ой грани. Тогда $a_{1}+a_{2}+...+a_{F}=2E$, но $a_{1}+a_{2}+...+a_{F}\geq 3F$; Значит, $2E\geq 3F$;

Теперь запишем так:

$V\leq E/3$

$F\leq 2E/3$;

Итого: $V-E+F\leq E/3-E+2E/3 =0$, что и требовалось.