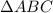 как:
как: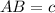 ;
;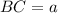 ;
;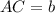 ;
;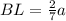 ;
;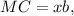 где
где  – некоторое число,
– некоторое число,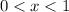 ;
;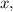 мы найдём и пропорцию, в которой
мы найдём и пропорцию, в которой 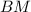 делит сторону
делит сторону 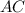 ;
;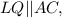 тогда по трём углам:
тогда по трём углам: 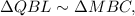
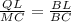 и
и 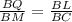 ;
;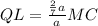 и
и 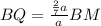 ;
;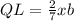 и
и 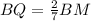 ;
;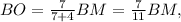 то:
то: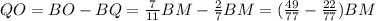 ;
;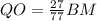 ;
;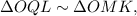 а значит:
а значит: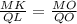 и
и 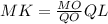 ;
;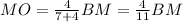 и по [1]
и по [1] 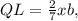 то:
то: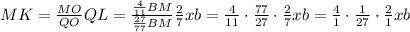 ;
;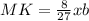 ;
;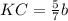 ;
;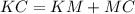 ;
;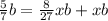 ;
;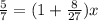 ;
;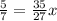 ;
;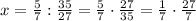 ;
;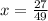 ;
;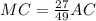 и
и 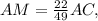 откуда ясно, что отношение, в котором точка
откуда ясно, что отношение, в котором точка 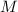 делит сторону
делит сторону 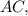 считая от точки
считая от точки 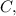 будет:
будет: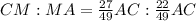 ;
;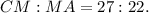
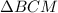 с секущей
с секущей 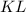 :
: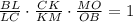 ;
;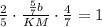 ;
;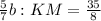 ;
;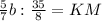 ;
;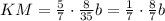 ;
;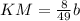 ;
;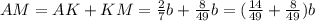 ;
;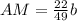 ;
;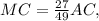 откуда ясно, что отношение, в котором точка
откуда ясно, что отношение, в котором точка 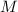 делит сторону
делит сторону 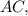 считая от точки
считая от точки 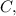 будет:
будет: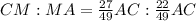 ;
;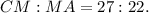
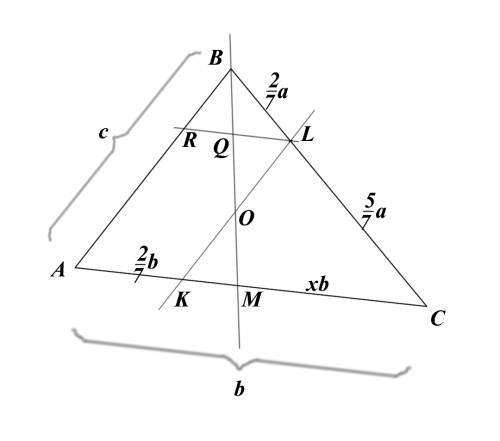
48/(Vк+Vр) + 48/(Vк-Vр) = 7 (1)
Возмём плот. До момента встречи он проплыл со скоростью Vр по течению 12 км. время плота до встречи 12/Vр.
А катер плыл 48 км по течению со скоростью Vк+Vр и 48-12=36 км со скоростью Vк-Vр, время катера до встречи 48/(Vк+Vр) + 36/(Vк-Vр).
так как они плыли одинаковое время до встречи приравняем
12/Vр =48/(Vк+Vр) + 36/(Vк-Vр) (2)
и того у нас система 2х уравнений (1) и (2) с 2мя неизвестными и решаем