1) Пусть G - точка пересечения медиан AD, BE и CF. Площадь треугольника ABE равна половине площади треугольника ABC, так как у этих треугольников высоты, проведенные из вершины B, равны, а основание AE в два раза меньше основания AC. Далее, поскольку медианы в точке пересечения делятся в отношении 2 к 1, считая от вершины, площадь треугольника ABG в два раза больше площади треугольника AGE, то есть площадь ABG - это 2/3 площади ABE, то есть (23)·(1/2)=1/3 площади ABC. Этим мы доказали, что треугольники ABG, BCG и CAG равновелики. Докажем теперь, что если для некоторой точки M, лежащей внутри треугольника, площади ABM, BCM и CAM равны, то M=G. Если это не так, то точка M лежит внутри одного из треугольников ABG, BCG, CAG, или на одной из сторон AG, BG, CG. Если точка M лежит внутри ABM или на AG или на BG, площадь ABM будет меньше площади ABG, а тогда треугольники ABM, BCM и CAM не будут равновеликими. Аналогично рассматриваются остальные случаи.
2) Воспользуемся формулой Пика, по которой площадь многоугольника с вершинами в узлах клетчатой бумаги со стороной квадратов 1 равна
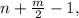
где n - количество узлов внутри многоугольника, m - число узлов на сторонах многоугольника и в его вершинах. В нашем случае n=1, m=3, поэтому площадь треугольника ABC равна 1+3/2-1=3/2. По той же формуле площади треугольников ABO, BCO, CAO равны 0+3/2-1=1/2, поэтому эти треугольники равновелики, а тогда по первому пункту O является точкой пересечения медиан.
Мы предположили, что стороны клеток равны 1. Если это не так, можно дополнительно рассмотреть клетчатую бумагу со стороной 1 и треугольник, подобный нашему, с вершинами в узлах новой решетки. Для нового треугольника утверждение доказано, а тогда и для исходного утверждение также справедливо. Другая возможность рассуждения состоит в введении новой единицы длины, равной стороне клетки. Тогда формула Пика оказывается справедлива и для такой бумаги.
очевидно при n = 1 не существует графа с 2 ребрами, поэтому n ≥ 2
степень вершины - количество всех ребер, выходящих из вершины deg(v)
сумма степеней всех вершин равна удвоенному количеству всех ребер
т.е. в данном графе сумма степеней вершин
будем доказывать от противного. предположим такого ребра нет.
рассмотрим любые 4 вершины, чтобы среди них не было ребра, которое принадлежит двум циклам длины 3, среди них может быть проведено не более 4 ребер, как бы не проводили пятое, всегда оно дополнит второй цикл.
поэтому сумма степеней всех вершин среди любых четырех не превосходит 4*2 = 8
рассмотрим четверки:
сложим все неравенства и получим, что
4*deg(V) ≤ 16n
deg(V) ≤ 4n
но deg(V) по условию равно 2n² + 2
2n² + 2 ≤ 4n
2(n-1)² ≤ 0
неравенство может выполниться только при n = 1, но как уже было отмечено, этот случай не удовлетворяет по условию.
Значит, наше предположение было не верно.
ответ: доказано.