точка A(1;-2) расположена вне окружности
Пошаговое объяснение:
Решим задание через определение степени точки относительно окружности
Степенью точки относительно данной окружности называется разность

d — расстояние от точки до центра окружности,
R — радиус окружности.
Точки имеют следуюющие степени в зависимости от расположения:
- вне окружности - положительную,
- внутри окружности - отрицательную,
- на окружности - нулевую.
Общее уравнение окружности задается уравнением
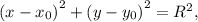
где (х0, у0) - координаты центра окружности
R - ее радиус.
В нашем случае:
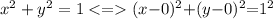
Следовательно,
радиус окружности R = 1;
центр окружности O = О(0; 0)
Теперь вычислим степень точки A(1;-2) относительно этой окружности:

Итак мы выяснили, что d² - R² > 0 =>
=> точка A(1;-2) расположена вне окружности.
1302 км
Пошаговое объяснение:
Расстояние от Москвы до поселка Калья Свердловской области составляет 1984 километра. Автомобиль выехал из Москвы и в первый день проделал 0,25 всего пути. Во второй день из-за плохой погоды автомобиль проехал всего 0,125 оставшегося пути. Сколько нужно проехать за третий день, чтобы добраться до поселка Калья?
Расстояние за 1-й день:
0,25 * 1984 = 496 км.
Оставшееся расстояние:
1984 - 496 = 1488 км.
Расстояние за 2-й день:
0,125 * 1488 = 186 км.
Найдем, сколько нужно проехать за третий день:
1984 - 496 - 186 = 1302 км.
С = 2 * π * r = π * d = 3.14 * 1.8 = 5,65;
Округляя до целых получим:
C = 6.
ответ: 6.