S = v * t - формула пути. S = АВ = ВА (км) - расстояние между пристанями х (км/ч) - собственная скорость катера v = х + 2 (км/ч) - скорость катера по течению реки; t = 6 (ч) - время в пути v = х - 2 (км/ч) - скорость катера против течения реки; t = 7,5 (ч) - время Уравнение: (х + 2) * 6 = (х - 2) * 7,5 6х + 12 = 7,5х - 15 7,5х - 6х = 12 + 15 1,5х = 27 х = 27 : 1,5 х = 18 (км/ч) - собственная скорость катера (18 + 2) * 6 = (18 - 2) * 7,5 = 120 (км) - расстояние между пристанями ответ: 18 км/ч - собственная скорость катера.
1) Пусть Х - масса одного утёнка, кг У - масса одного гуся, кг
Тогда можно составить систему уравнений
Вычтем из первого уравнения втрое
ответ: масса оного гусёнка 0,5 кг или 500 г
2) Дана последовательность натуральных чисел Учитывая, что ряд заканчивается четным числом, значит количество четных и нечетных чисел одинаковое, т.е. 2010 / 2 = 1005 шт. - нечётное число
Таким образом:
1) Вычеркивая в любом порядке только одни чётные числа, полученная разность любого их количества - есть число чётное
2) Вычеркивая в любом порядке только одни нечётные числа, полученная разность их нечётного количества - есть число нечётное
3) Вычеркивая в любом порядке только одно чётное и одно нечётные число, полученная разность их нечётного количества - есть число нечётное
4) В результате вычеркивания в конце всегда остается одно число чётное и одно число нечётное, а их разница - есть число нечётное и не может быть равно нулю!
Значит если в конце останется один нуль,то где-то была допущена ошибка. Что и требовалось доказать Дана последовательность натуральных чисел 1,2,3,....2007,2008,2009,2010 - данный ряд представляет собой арифметическую прогрессию, где
Найдем сумму арифметической прогрессии - нечётное число!
Сумма арифметической прогрессии и это же утверждении справедливо и для разности - есть всегда число нечётное, таким образом в конце не может остаться один нуль, т.к. ноль число чётное! Что и требовалось доказать!
Пошаговое объяснение:
Так как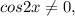 то
то
Так как должны выполняться условия :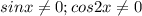 , то
, то