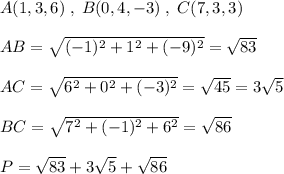
P = √83 + √86 + 3√5
Пошаговое объяснение:
AB = (0 - 1; 4 - 3; -3 - 6) = (-1; 1; -9)
|AB| = √(1 + 1 + 81) = √83
BC = (7 - 0; 3 - 4; 3 - (-3)) = (7; -1; 6)
|BC| = √(49 + 1 + 36) = √86
AC = (7 - 1; 3 - 3; 3 - 6) = (6; 0; -3)
|AC| = √(36 + 0 + 9) = √45 = 3√5
P = |AC| + |AB| + |BC| = √83 + √86 + 3√5
Алгоритм:
а)взять первую производную
б) вычислить значения х, при которых первая производная равна 0
в) вычислить вторую производную и её знаки при значения х которые получили в пункте(б)
г) исследовать поведение второй производной в этих точках.
Итак:
первая производная: 3х²-24х
3х²-24х=0 при х=0 и х=8
вторая производная: 6х-24 при х=0 меньше 0, а это значит, что функция у(максимум)(т.е выпуклость)=1 при х=0
6х-24 при х=8 больше 0, а это значит, что функция у(минимум)(т.е вогнутость)=-255(но нас это по условию задачи не интересует)
Удачи!
Пошаговое объяснение: