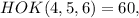
 где
где  – некоторое целое число.
– некоторое целое число.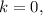 тогда
тогда 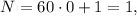 но
но  не делится на
не делится на  а значит не подходит.
а значит не подходит.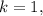 тогда
тогда 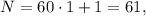 но
но 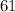 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 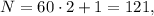 но
но 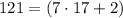 не делится на
не делится на  а значит не подходит.
а значит не подходит.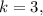 тогда
тогда 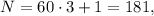 но
но 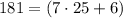 не делится на
не делится на  а значит не подходит.
а значит не подходит.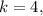 тогда
тогда 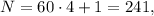 но
но 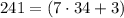 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 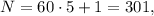 и
и 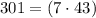 – делится на
– делится на  а значит подходит !
а значит подходит !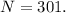
 где
где  – некоторое целое число.
– некоторое целое число.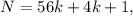 где
где  – некоторое целое число.
– некоторое целое число.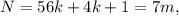 где
где  и
и 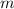 – некоторые целые числа.
– некоторые целые числа.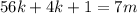 ;
;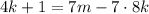 ;
;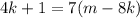 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: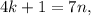 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.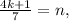 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 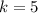 ;
;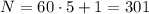 ;
; где
где  – некоторое целое число.
– некоторое целое число.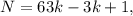 где
где  – некоторое целое число.
– некоторое целое число. где
где  и
и 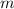 – некоторые целые числа.
– некоторые целые числа.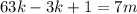 ;
;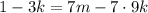 ;
;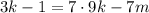 ;
;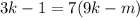 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: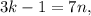 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.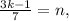 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 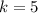 ;
;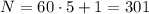 ;
;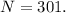
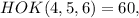
 где
где  – некоторое целое число.
– некоторое целое число.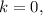 тогда
тогда 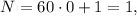 но
но  не делится на
не делится на  а значит не подходит.
а значит не подходит.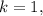 тогда
тогда 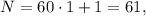 но
но 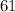 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 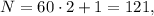 но
но 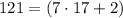 не делится на
не делится на  а значит не подходит.
а значит не подходит.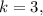 тогда
тогда 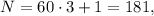 но
но 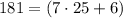 не делится на
не делится на  а значит не подходит.
а значит не подходит.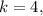 тогда
тогда 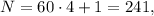 но
но 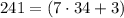 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 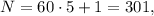 и
и 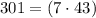 – делится на
– делится на  а значит подходит !
а значит подходит !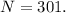
 где
где  – некоторое целое число.
– некоторое целое число.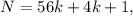 где
где  – некоторое целое число.
– некоторое целое число.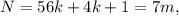 где
где  и
и 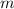 – некоторые целые числа.
– некоторые целые числа.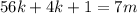 ;
;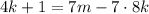 ;
;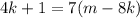 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: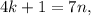 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.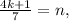 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 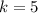 ;
;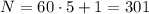 ;
; где
где  – некоторое целое число.
– некоторое целое число.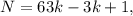 где
где  – некоторое целое число.
– некоторое целое число. где
где  и
и 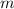 – некоторые целые числа.
– некоторые целые числа.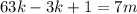 ;
;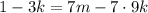 ;
;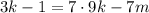 ;
;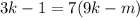 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: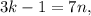 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.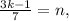 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 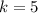 ;
;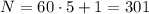 ;
;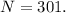
5 и 5; 5 и 4; 5 и 3; 5 и 2; 5 и 1
4 и 4; 4 и 3; 4 и 2; 4 и 1
3 и 3; 3 и 2; 3 и 1
2 и 2; 2 и 1
1 и 1
( первая цифра это количество закрашенных частей левого прямоугольника, а правая-количество закрашенных частей правого прямоугольника)
Пошаговое объяснение:
Дроби, у которых числитель больше или равен знаменателю, называются неправильными.