ответ: а) у=C₁eˣ+C₂e²ˣ б)у=C₁eˣ+C₂хeˣ в) у=C₁eˣCos2x+C₂eˣSin2x
Пошаговое объяснение:№1
а) y"-3y'+2y=0
составим характеристическое уравнение: k²-3k+2=0
D=9-8=1>0 ⇒ k₁=(3+1)/2=2, k₂=(3-1)/2=1
Следовательно, фундаментальную систему решений составляют функции:
y₁=eˣ , y₂=e²ˣ
Значит общее решение однородного уравнения имеет вид: у=C₁eˣ+C₂e²ˣ
б) y"-2y'+y=0
составим характеристическое уравнение: k²-2k+1=0
D=4-4=0 ⇒ k₁=1, k₂=1
Получили корень характеристического уравнения 1 кратности 2.
Следовательно, фундаментальную систему решений составляют функции:
y₁=eˣ , y₂=хeˣ
Значит общее решение однородного уравнения имеет вид: у=C₁eˣ+C₂хeˣ
в) y"-2y'+5y=0
составим характеристическое уравнение: k²-2k+5=0
D=4-20=-16=(4i)²<0 ⇒ k₁=(2+4i)/2=1+2i, k₂=1-2i (корни-комплексные числа)
Следовательно, фундаментальную систему решений составляют функции:
y₁=eˣ·Cos2x , y₂=eˣ·Sin2x
Значит общее решение однородного уравнения имеет вид: у=C₁eˣCos2x+C₂eˣSin2x
В решении.
Пошаговое объяснение:
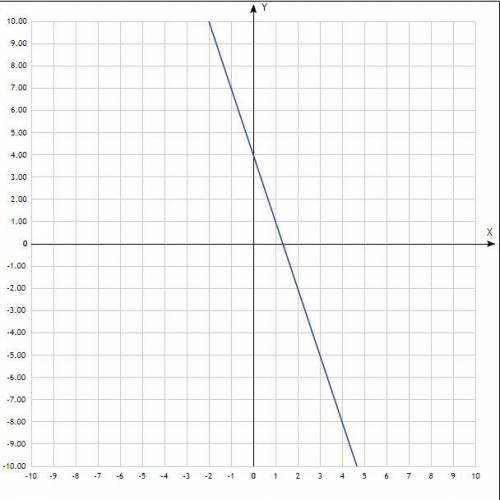
Постройте график функции y = -3x+4.
Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = -3х + 4;
Таблица:
х -1 0 1
у 7 4 1
Пользуясь графиком, найдите:
1. Значение функции, если значение аргумента равно 2;
При х = 2 у = -2;
2. Значение аргумента, при котором значение функции равно 7;
у = 7 при х = -1.
-1,9/6,3 - 3x > 0
-1,8/2,7x < 13,5
-1,9/6,3 > 3х
-1,8 < 13,5 • 2,7х
-1,9 > 6,3 • 3х
-1,8 < 36,45х
-1,9 > 18,9х
36,45х > -1,8
18,9х < -1,9
3645/100 • х > -18/10
189/10 • х < -19/10
х > -18•100/(3645•10)
х < -19•10/(189•10)
х > - 180/3645
х < - 19/189
х > -4/81
х < -19/189
х > -7•4(7•81)
х < -3•19/(3•189)
х > -28/567
х < - 57/567
ответ:
х > -28/567
и
х < - 57/567
или
{-∞; -57/567} и {-28/567; ∞}