Касательные — это прямые вида 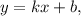 где
где 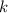 и
и 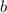 — некоторые числа.
— некоторые числа.
Если прямые 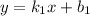 и
и 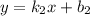 параллельны, то
параллельны, то 
За коэффициент 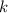 касательной отвечает производная
касательной отвечает производная 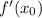 функции в точке с абсциссой
функции в точке с абсциссой 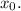
1. Найдем производную функции 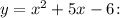
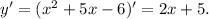
2. Определим абсциссу точки касания.
2.1. Для прямой 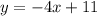 коэффициент
коэффициент 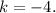
2.2. Для функции  касательная в данной точке по геометрическому смыслу производной имеет угловой коэффициент
касательная в данной точке по геометрическому смыслу производной имеет угловой коэффициент 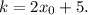
2.3. Поскольку прямая 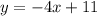 параллельна касательной к графику функции
параллельна касательной к графику функции 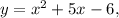 то:
то:
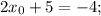
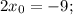
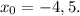
Таким образом, 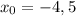 — абсцисса точки касания к графику функции
— абсцисса точки касания к графику функции 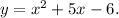
ответ: 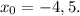
1. Записать двойной интеграл в виде повторного, расставив пределы интегрирования в том и другом порядке:
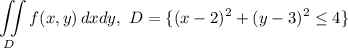
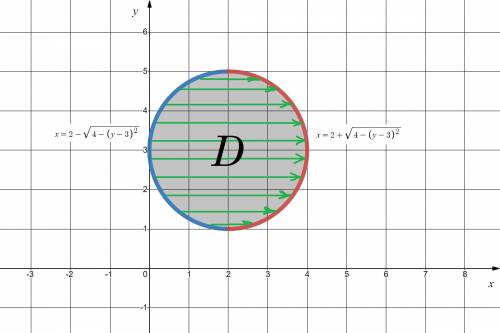
Решение. Изобразим область 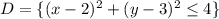 (см. вложение 1).
(см. вложение 1).
Имеем:
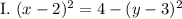
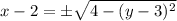
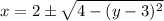 — полудуги окружности слева и справа.
— полудуги окружности слева и справа.
Тогда повторный интеграл:
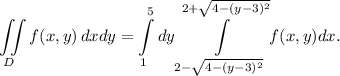
Пояснение. Первый слева интеграл имеет пределы интегрирования от наименьшего значения до наибольшего значения по оси 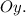 Второй интеграл имеет пределы интегрирования по движению в горизонтальном направлении от дуги
Второй интеграл имеет пределы интегрирования по движению в горизонтальном направлении от дуги 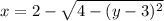 до дуги
до дуги 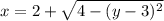 (см. вложение 2).
(см. вложение 2).
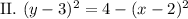
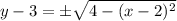
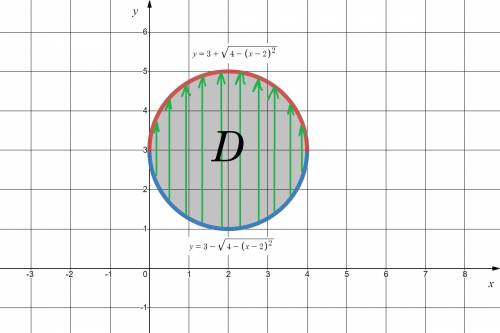
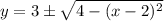 — полудуги окружности сверху и снизу.
— полудуги окружности сверху и снизу.
Тогда повторный интеграл:
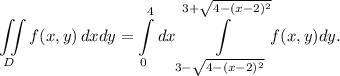
Пояснение. Первый слева интеграл имеет пределы интегрирования от наименьшего значения до наибольшего значения по оси 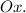 Второй интеграл имеет пределы интегрирования по движения в вертикальном направлении от дуги
Второй интеграл имеет пределы интегрирования по движения в вертикальном направлении от дуги 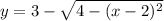 до дуги
до дуги 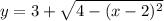 (см. вложение 3).
(см. вложение 3).
2. Найти частные производные второго порядка функции:
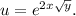
Решение. Найдём частную производную первого порядка по 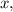 считая что
считая что  — переменная,
— переменная, 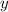 — постоянная:
— постоянная:

Найдём частную производную первого порядка по 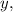 считая что
считая что 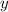 — переменная,
— переменная,  — постоянная:
— постоянная:

Найдём частную производную второго порядка по 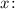
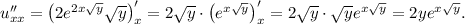
Найдём частную производную второго порядка по 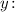
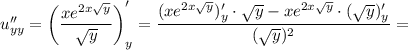

Найдём частную производную функции 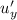 по
по 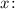
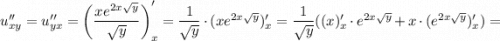
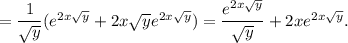
3. Исследовать на сходимость ряд с общим членом 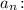
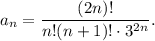
Решение. Найдем 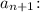
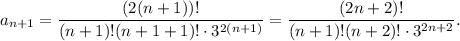
Найдем предел:
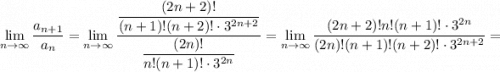
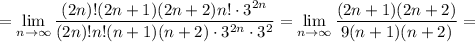
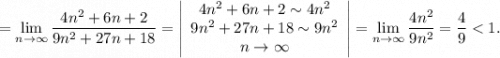
Таким образом, по признаку Даламбера ряд с общим членом 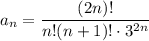 является сходящим.
является сходящим.

ответ: 8/6<х/6<5/2=15/6 или 8<х<15. Искомые числа 9, 10, 11, 12, 13, 14.
Пошаговое объяснение: