Поскольку не имеет значения порядок расположения данных принадлежностей, это не размещение, т.к. количество принадлежностей, входящих в комбинацию, не совпадает с общим количеством 2+4+5, это не перестановка, следовательно, это сочетания. Из двух карандашей надо выбрать один, это число сочетаний из 2 по одному. Оно равно двум. Из 4 ручек выбрать одну можно с из пяти блокнотов один с а т.к. необходимо посчитать выбора И карандаша, И ручки, И блокнота, используем правило умножения, т.е. общее число равно 2*4*5=40
х - скорость 1 авто (1 - его путь )
х-12 -скорость 2 авто на 1-ой половине пути (1/2 или 0,5 - пройденный путь)
72км/час -скорость 2 авто на 2-ой половине пути (тоже 0,5 - пройденный путь)
1/х - время 1 авто
0,5/ х-12 + 0,5/72 - время 2 авто
Так как время одно, то составим уравнение:
1/х =0,5/ х-12 + 0,5/72
1/х - 0,5/ х-12 - 0,5/72 =0
Приведём к общему знаменателю: х*(х-12)*72
36х+0,5х²-6х-72х+864=0
0,5х²-42х+864=0
Д=42²-4*0,5*864=1764-1728=36
х1=42-6 / 0,5*2 =40 - не подходит к условию задачи, т.к. д.б. >45
х2=42+6 / 0,5*2 =48 км/час - скорость 1 автомобиля
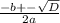. Например: х²-9х+8=0, D=(-9)²-4*1*8, D=81-32, D=49, x1=(9-√49)/2=(9-7)/2=2/2=1, x2=(9+√49)/2=(9+7)/2=16/2=8. Также есть неполные квадратные уравнения (без переменной с), решаются они выносом общего множителя за скобки. Например: 3х-х²=0, х(3-х)=0, х1=0, 3-х=0, х2=3; 3х²+х=0, х(3х+1)=0, х1=0, 3х+1=0, 3х=-1, х=-1/3; 4х²+20х=0, 4х(х+5)=0, 4х=0, х1=0, х+5=0, х=-5.
Пошаговое объяснение: