S параллелограмма ABCD = 140 см^2
Пошаговое объяснение:
MN-средняя линия трапеции AKCD
MN=(KC+AD)/2
AD=2MN-KC
AD=2*13-6=20 см
AD=BC=20 см
BK=BC-KC=20-6=14 см
угол ВАК= углу КАD, так как АК- биссектриса
угол KAD= углу ВКА, так как ABCD-параллелограмм
AD║BC, AK-секущая
угол KAD= углу ВКА - накрест лежащие.
Тогда угол ВАК=углу ВКА, следовательно треугольник АВК - равнобедренный (углы при основании равны)
Получается , что АВ=ВК=14 см
угол А = 30 градусов (по условию)
S (ABCD) =AB*AD*sin30 градусов=14*20*1/2=140 см^2

наименьшее значение функции на отрезке [-3 ; 0] равно -193
Пошаговое объяснение:
8)
f(x) = 5x³ - 4x +ln x; значение производной при х = 2
найдем производную
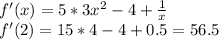
9)
f(x) = 2x³ -2x² - 36x +2; наименьшее значение на отрезке [-3; 0]
посмотрим на существование и непрерывность функции. найдем производную
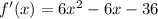
найдем критические точки. приравняем производную к 0 и найдем корни
f'(x) = 6x² -6x - 36 = 0
x₁ = 2 ; x₂ = -3
точка х₁ = 2 не принадлежит нашему отрезку [-3; 0]
поэтому посчитаем значение функции в т. х = -3 и на конце отрезка в т.х=0
f(0) = 2
f(-3) = 2(-3)³ - 3(-3)² -36(-3) +3 = -193
log ab = log a + log b
(log(5) (125x)*log(3) (81x)) / (x² - |x|) ≤ 0
одз 125x > 0 x > 0
81x > 0 x > 0
x² - |x| ≠ 0 x ≠ 0 x ≠ -1 x ≠ 1
x∈(0, 1) U (1, +∞)
так как x > 0 модуль снимаем как х
((log(5) (125) + log(5) x)*(log(3) (81) + log(3) x) / x(x - 1) ≤ 0
81 = 3^4
125 = 5^3
(3 + log(5) x)(4 + log(3) x) / x(x - 1) ≤ 0
log(5) x = -3 x = 5^(-3) = 1/125
log(3) x = -4 x = 3^(-4) = 1/81
(0) [1/125][1/81](1)
x ∈ (0, 1/125] U [ 1/81, 1)