(d - 295) · 13 = 260
d-295=260:13
d-295=20
d=295+20
d=315
25. (540 – s) = 2500
540-s=2500:25
540-s=100
s=540-100
s=440
t: (6000 – 5996) = 600
t:4=600
t=600*4
t=2400
(471 + h) : 11 = 781
471+h=781*11
471+h=8591
h=8591-471
h=8120
Пошаговое объяснение:
Вспомним признаки делимости
2 Последняя цифра числа а делится на 2
3 Сумма цифр числа а делится на 3
4 Число, из двух последних цифр числа а, делится на 4
5 Число а оканчивается цифрой 0 или 5
6 Число а делится на 2 и на 3
7 Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7
8 Число, из трёх последних цифр числа а, делится на 8
9 Сумма цифр числа а делится на 9
10 Число а оканчивается цифрой 0
Значит в числе должен быть 0, тогда оно будет делиться на 2,5,0, 10;
6 – тогда оно будет делиться на 4,3,6,8 и 3- тогда будет делится на 9 и 7
Подбираем , пусть число будет 360 – делится на 2,3,4,5,6,8,9,10 и число 630 – делится на 7
Значит искомые три цифры 3,6,0
ответ: 20
Определение: Диагональ – это отрезок, соединяющий любые две несмежные вершины многоугольника
Объяснение:
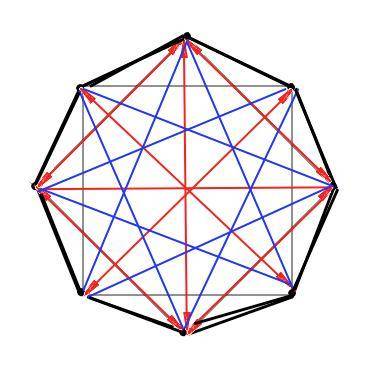
Рассмотрим рисунок выпуклого восьмиугольника, данный в приложении. Каждая вершина соединяется отрезками с 7 другими. Но два из этих отрезков не являются диагоналями. Получается, что из каждой вершины выходит диагоналей на 3 меньше, чем количество всех вершин. Для пятиугольника - из каждой вершины выходят 5-3 =2 диагонали. для квадрата из каждой вершины 4-3=1 диагональ. У треугольника диагоналей вовсе нет. Но! Каждая диагональ посчитана дважды ( отмечено на красных диагоналях рисунка). Следовательно, это количество нужно разделить на 2.
Таким образом: формула лля нахождения числа диагоналей многоугольника d =n(n-3)/2, где d – число диагоналей, n – число сторон (вершин) многоугольника.
Число диагоналей восьмиугольника d=8•(8-3)/2=20 ( диагоналей(
Пошаговое объяснение: