1 ведро-?, на 10кг>, чем во 2ом
2ведро-
3ведро-?, в 2 раза <, чем в 1ом
Всего в трёх ведрах -240кг
Пусть х кг во втором ведре
Тогда х+10- первое ведро
Тогда (х+2):2- третье ведро
Х+(х+10)+((х+2):2)=240
Пошаговое объяснение:
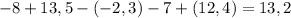
Пошаговое объяснение:
Для начала распишем пример. Там, где 2 минуса, напишем +, т.к. когда рядом стоят 2 минуса, будет плюс.
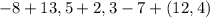
Далее сложили все минусы и все плюсы отдельно и сложим их.
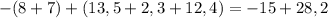
Теперь нужно сложить отрицательное число с положительным числом. Для этого нужно от большего модуля из чисел отнять меньший и в результате написать перед ответом знак большего модуля, из которого отнимали.
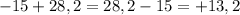
Плюс в ответе необязательно писать, по умолчанию не нужно. ответ: 13,2
Если понравилось решение, то можете поставить лайк :-)
ответ:Из истории синуса IV в.- Индия (Ариабхата)-- «ардхаджива» (полутетива) IV в.- Индия (Ариабхата)-- «ардхаджива» (полутетива) Вычисления синуса были связаны с полухордами в окружности, которые называли архаджива (инд. яз.) Вычисления синуса были связаны с полухордами в окружности, которые называли архаджива (инд. яз.) Термин сократился до «джива» Термин сократился до «джива» - при переводе арабы заменили его на«джайб» (впадина) - при переводе арабы заменили его на«джайб» (впадина) IV в.- Индия (Ариабхата)-- «ардхаджива» (полутетива) IV в.- Индия (Ариабхата)-- «ардхаджива» (полутетива) Вычисления синуса были связаны с полухордами в окружности, которые называли архаджива (инд. яз.) Вычисления синуса были связаны с полухордами в окружности, которые называли архаджива (инд. яз.) Термин сократился до «джива» Термин сократился до «джива» - при переводе арабы заменили его на«джайб» (впадина) - при переводе арабы заменили его на«джайб» (впадина) XVII в. - Уильям Отред, Леонард Эйлер вводят обозначение термина- «sin» XVII в. - Уильям Отред, Леонард Эйлер вводят обозначение термина- «sin».
Из истории косинуса Слово косинус намного моложе. Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. дополнительный синус.Косинус – это сокращение латинского выражения completely sinus, т. е. дополнительный синус (или иначе синус дополнительной дуги; (или иначе синус дополнительной дуги; cos А = sin( 90( - (А)). cos А = sin( 90( - (А)).
Из истории тангенса Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом и астрологом Регимонтаном (1467 г.). Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом и астрологом Регимонтаном (1467 г.). Название «тангенс», происходящее от латинского tanger (касаться), появилось Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности). касательная к единичной окружности).
Пошаговое объяснение: