Чтобы из числа можно было сделать все шесть различных двухзначных чисел, необходимо, чтобы исходное число было трехзначным и все цифры в нем были разные, представим это число в виде 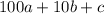 .
.
А сумма всех шести различных двухзначных чисел будет такая:
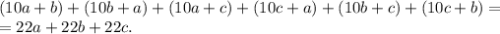
При этом (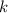 натуральное):
натуральное):
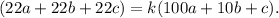
Представим теперь, что 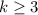 , то есть:
, то есть:
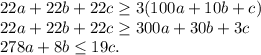
Но это противоречие, так как правая часть по-любому больше левой, а здесь она меньше. Поэтому 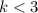 .
.
Итак, нужно рассмотреть два случая:
1). 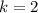 . Тогда:
. Тогда:
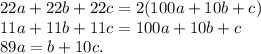
Нетрудно понять, что в натуральных однозначных числах здесь всего одно решение: 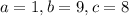 .
.
А нужное число - это 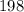 .
.
2). Случай посложнее: 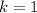 .
.
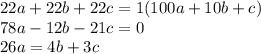
Если 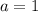 уравнение принимает вид
уравнение принимает вид 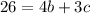 , и, тогда в вышеуказанных условиях у него такое одно решение:
, и, тогда в вышеуказанных условиях у него такое одно решение: 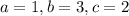 . Число -
. Число - 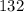 .
.
Ну а теперь пусть 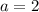 и
и 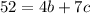 . Здесь методом подбора:
. Здесь методом подбора: 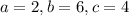 . А число -
. А число - 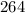 .
.
И последний случай 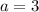 , то есть
, то есть 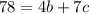 , где, подбором,
, где, подбором, 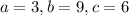 . Число
. Число 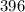 .
.
Делаем вывод, что Вася богатый и у него в доме четыре (по крайней мере!) квартиры.
Первоначально в бригаде было x рабочих, которые работали по y часов в день.
Производительность всей бригады 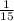 всей работы в день или
всей работы в день или  всей работы в час.
всей работы в час.
Производительность одного рабочего 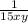 всей работы в час.
всей работы в час.
Если бригадир наймет девять дополнительных рабочих, и при этом в день бригада будет работать на 2 часа меньше, то работа будет выполнена за 12 дней, то есть
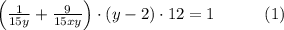
Если бригадир уволит пятерых рабочих из первоначального состава бригады, то, чтобы окончить работу за 20 дней, бригаде придётся трудиться на 2 часа в день больше, то есть
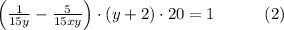
Составим и решим систему уравнений (1) и (2):

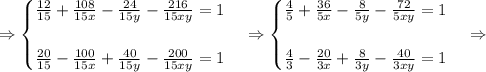
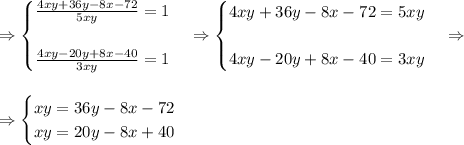
Вычтём из первого уравнения второе:
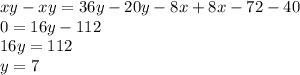
Подставим значение y в любое из двух уравнений систему (например, во второе) и вычислим x:
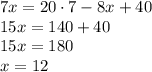
Тогда
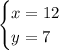
ответ: первоначально в бригаде было 12 рабочих, которые работали по 7 часов в день.
Пошаговое объяснение:
1) 3,62 - 1,51 = 2,11
1) 14,3 + 2,6 = 16,9
2) 0,27 +6,13 = 6,4
2) 74,5 - 3,503 = 70,997
3) 25 + 4,94 = 29,94
3) 0,8 - 0,25 = 0,55
4) 51,9 + 3,057 = 54,957
4) 425 - 43,17 = 381,83
5) 207,2 + 3,8 = 203,4
5) 8,034 - 7,34 = 0,694
6) 0,48 +0,2 = 0,68
6) 631.17 - 1,07 = 630,1
7) 61,3 + 207 = 268,3
7) 10,273 - 5,49 = 4,783
8) 0,004 + 0,0320 = 0,036
8) 0,01 – 0,001 = 0,009
1) 3,5 + 12,3 = 15,8
2) 4,1 - 3,7 = 0,4
3) 6,8 - 4 = 2,8
4)100 - 0,2 = 99,8