100 человек
Пошаговое объяснение:
Число тех, кто не решил ни одной задачи возьмём за х
800 задач решили по алгебре
700 задач решили по геометрии
600 задач решили по тригонометрии
А+Г=600 школьников
А+Т=500 школьников
Г+Т=400 школьников
А+Г+Т= 300 школьников
1) А+Г+Т=800+700+600=2100 -всего решили задач по А,Г,Т
т.к. 300 человек (которые решили по три задачи) учтены при А+Г, А+Т, Г+Т определим сколько человек решили по две задачи.
2) А+Г=600 - 300=300 чел решили только две задачи А+Г
3) А+Т=500- 300 =200 чел решили только две задачи А+Т
4) Г+Т=400-300= 100 чел. решили только две задачи Г+Т
5) 300+200+100=600 человек решили две задачи
6) 600*2+300*3=1200+900=2100 задач решили школьники (которые решили по две и по три задачи)
7)2100-2100=0- задач решили школьники (которые решили только по одной задачи)
8) 300+600=900 школьников решили две и более задач
9) 1000-900=100 школьников ничего не решили
ответ: 100 школьников ничего не решили.
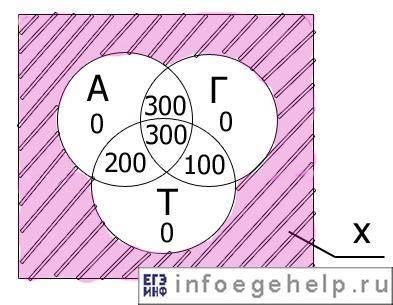
Ниже прикрепил картинку, чтобы было видно визуально
Прежде чем вычислить сумму квадратов этих чисел,
найдём эти числа, для этого обозначим эти числа за (х) и (у),
тогда согласно условия задачи:
х+у=15 (1)
Средне-арифметическое этих двух чисел равно:
(х+у)/2
Средне геометрическое этих двух чисел равно:
√(х*у)
25% средне геометрического числа равно:
25% *√(ху) :100%=0,25*√(ху)=0,25√(ху)
Согласно условия задачи составим второе уравнение:
(х+у)/2 - √(ху)=0,25√(ху)
(х+у)/2=0,25√(ху)+√(ху)
(х+у)/2=1,25√(ху)
(х+у)=2*1,25√(ху)
х+у=2,5√(ху) (2)
Решим получившуюся систему из двух уравнений:
х+у=15
х+у=2,5√(ху)
Из первого уравнения системы уравнений найдём значение (х)
х=15-у -подставим значение (х) во второе уравнение
15-у+у=2,5√[(15-y)*y]
15=2,5√(15y-y²) чтобы избавиться от иррациональности в правой части, возведём левую и правую части уравнения в квадрат:
225=6,25*(15у-у²)
225=93,75у-6,25у²
6,25у²-93,75у+225=0
у1,2=(93,75+-D)/2*6,25
D=√(93,75² -4*6,25*225)=√(8789,0625-5625)=√3164,0625=56.25
у1,2=(93,75+-56,25)/12,5
у1=(93,75+56,26)/12,5=150/12,5=12
у2=(93,75-56,25)/12,5=37,5/12,5=3
Подставим значения (у1) и (у2) в х=15-у
х1=15-12=3
х2=15-3=12
Из получившихся чисел можно сделать вывод, что эти два числа 12 и 3
Отсюда сумма квадратов этих чисел равна:
12²+3²=144+9=153
ответ: 153