Так как всего цифр в числе 4, то в нем могут быть две различные цифры (одна повторяется три раза, а другая один раз) или четыре различные цифры.
Первый вариант. В числе только две различные цифры: одна повторяется три раза, а другая один раз.
На первое место мы можем поставить любую цифру, кроме нуля - 9 вариантов. В качестве другой цифры этого числа можно использовать любую, кроме уже использованной - 9 вариантов. Поскольку уникальная цифра может стоять на любой из 4 позиций, то общее число таких чисел:
Второй вариант. В числе четыре различные цифры.
На первое место мы можем поставить любую цифру, кроме нуля - 9 вариантов. На второе место - любую, кроме использованной на первом шаге - 9 вариантов. На третье место - любую, кроме использованных двух - 8 вариантов. На четвертое место - любую, кроме использованных трех - 7 вариантов. Общее число таких чисел:
Находим производную функции f(x)=2x²-x⁴+1. y ' = -4x³ + 4x = -4x(x² - 1). Приравниваем производную нулю: -4x(x² - 1) = 0. Отсюда получаем критические точки: х₁ = 0, x² - 1 = 0 x² = 1. х₂ = 1, х₃ = -1. На проміжку [-2;0] имеется 2 критические точки: х = -1 и х = 0. Исследуем значение производной вблизи этих точек. х = -1.5 -1 -0.5 0 0.5 y '=-4x³+4x 7.5 0 -1.5 0 1.5. В точке х = -1 переход от + к -, значит, это максимум, а в точке х = 0 переход от - к +, значит, это минимум.
Так как всего цифр в числе 4, то в нем могут быть две различные цифры (одна повторяется три раза, а другая один раз) или четыре различные цифры.
Первый вариант. В числе только две различные цифры: одна повторяется три раза, а другая один раз.
На первое место мы можем поставить любую цифру, кроме нуля - 9 вариантов. В качестве другой цифры этого числа можно использовать любую, кроме уже использованной - 9 вариантов. Поскольку уникальная цифра может стоять на любой из 4 позиций, то общее число таких чисел: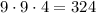
Второй вариант. В числе четыре различные цифры.
На первое место мы можем поставить любую цифру, кроме нуля - 9 вариантов. На второе место - любую, кроме использованной на первом шаге - 9 вариантов. На третье место - любую, кроме использованных двух - 8 вариантов. На четвертое место - любую, кроме использованных трех - 7 вариантов. Общее число таких чисел: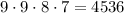
Итого: чисел удовлетворяющих условию: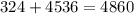
ответ: 4860