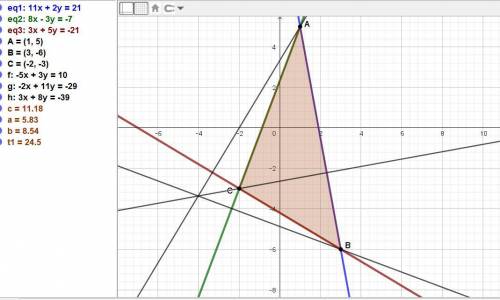
Даны уравнениям сторон треугольника:
11x+2y-21=0
8x-3y+7=0
3x+5y+21=0.
В уравнении перпендикулярной прямой коэффициенты А и В в уравнении вида Ах + Ву + С = 0 меняются на -В и А.
Возьмём первую сторону (пусть это АВ, получаем уравнение высоты из точки С: -2х + 11у + С = 0. Чтобы определить слагаемое С уравнения надо подставить координаты точки, через которую проходит прямая.
Находим вершины треугольника, решая системы из двух уравнений сторон. Точка А:
{11x+2y-21=0 |x(3) = 33x + 6y - 63 = 0
{8x-3y+7=0 |x(2) = 16x - 6y + 14 = 0
49x - 49 = 0, х = 49/49 = 1.
у = (21 - 11х)/2 = (21 - 11*1)/2 = 10/2 = 5. Точка А(1; 5).
Аналогично определяем точки: В(3; -6) и С(-2; -3).
Теперь находим С в уравнении высоты из точки С.
-2*(-2) + 11*(-3) + С = 0,
С = 33 - 4 = 29. Уравнение -2х + 11у + 29 = 0.
Аналогично находим уравнения высот из точек А и В.
Высота из точки А: -5х + 3у - 10 = 0,
из точки В: 3х + 8у + 39 = 0.
Чтобы сумму разделить на число, можно разделить на число каждое слагаемое и полученные частные сложить.
(а+b) : с = а:с + b:с
Рассмотрим пример №1.
Используем правило (наоборот) :
8:2 + 6: 2 = (8+6) :2
Сумма (8+6)
Делитель 2
Решим:
8:2 + 6: 2 = (8+6) :2 = 14:2 = 7
Аналогично решим другие примеры:
15:3 + 9 : 3 = (15 + 9) :3 = 24 :3 = 8
276:23 + 184:23 = (276 +184) :23 = 460 :23 = 20
21:7 + 28:7 = (21 +28) :7 = 49 : 7 = 7
15:5 +25:5 = (15 +25) : 5 = 40 : 5 = 8
116:29 +609:29 = (116+609):29 = 725 : 29 = 25