![\displaystyle\int(4\sqrt x+6x^2-5\sqrt[5]x)dx=\frac{8\sqrt {x^3}}{3}+2x^3-\frac{25\sqrt[5]{x^6}}{6}+C\\\\\int\frac{3}{2+2x^2}dx=\frac{3}{2}arctgx+C\\\\\int\frac{4}{13}x^5dx=\frac{2x^6}{39}+C](/tpl/images/1092/8437/b8b34.png)
ДАНО
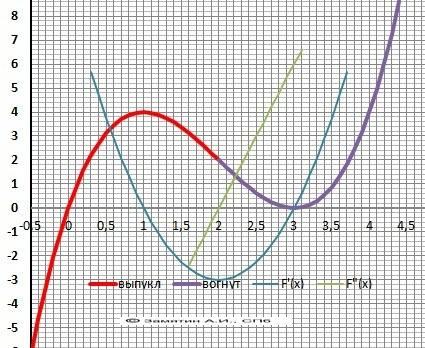
Y = x³ - 6x² + 9x
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
Вертикальных асимптот - нет.
2. Пересечение с осью Х. Y= 0 Корни: х₁,₂ =3, х₃ = 0.
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞.
Горизонтальной асимптоты - нет.
5. Исследование на чётность.Y(-x) ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 3*x² - 12*х+9 = 3*(х-1)*(х - 3).
Корни: х₁=1 , х₂ = 3.
7. Локальные экстремумы.
Максимум Ymax(11)= 4, минимум – Ymin(3)=0.
8. Интервалы монотонности.
Возрастает - Х∈(-∞;1)∪(3;+∞) , убывает = Х∈(1;3).
8. Вторая производная - Y"(x) = 6*(x - 2)=0.
Корень производной - точка перегиба Y"(2)= 2.
9. Выпуклая “горка» Х∈(-∞;2), Вогнутая – «ложка» Х∈(2;+∞).
10. Область значений Е(у) У∈(-∞;+∞)
11. Наклонная асимптота. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(oo)Y(x)/x = ∞. Наклонной асимптоты - нет
12. График в приложении.
В треугольнике 3 стороны,его периметр равен 46 5/8
Ав+ВЦ =31 1/4
Ав+АЦ =28 5/6
Обрати внимание-в этих двух равенствах два раза упоминается сторона АВ и по одному разу две другие стороны,одна АВ тут явно лишняя и сейчас мы ее узнаём
Для начала Сложим суммы четырёх сторон
3 1/4+28 5/16=3 4/16+28 5/16=59 9/16
И от этой суммы вычтем периметр- который является суммой трёх сторон
59 9/16-46 10/16=12 15/16
Это и есть сторона АВ
Теперь без проблем найдём другие стороны
Вс=31 1/4-АВ
ВС=31 1/4-12 15/16=31 4/16-12 15/16=
18 5/16
АЦ =28 5/16-12 15/16=15 6/16
Проверка
15 6/16+18 5/16+12 15/16=45 26/16=
46 10/16
Пошаговое объяснение: