Умова завдання:
26.
Запиши найбільше число одиничних
відрізків, що відповідають одному діленню
координатного променя, щоб можна було
відзначити числа:
20, 30, 40, 50, 80, 90,
Скільком поділкам відповідає число 50?

👇

Увидеть ответ

Ответ:

marina02427

16.02.2022

Найменшу подилку можна взяти 10

Пошаговое объяснение:

4,8(6 оценок)

Открыть все ответы

Ответ:

СешМАНИ

16.02.2022

Заведомо надо купить 4 синих шарика, 4 красных и 4 зелёных. Остаётся купить ещё 4 шарика, каждый из которых уже может быть любого из трёх цветов. Подсчитаем количество возможных вариантов.

1) Все 4 шарика одного цвета. Таких вариантов 3 – по числу цветов.

2) 3 шарика одного цвета, а четвёртый – другого. Первый цвет выбирается , второй – двумя. Всего 6 вариантов.

3) 2 шарика одного цвета, а два – другого. Таких вариантов 3.

4) 2 шарика одного цвета, один – другого и один – третьего. И таких вариантов 3.

Итого, 3 + 6 + 3 + 3 + 3 = 15 вариантов.

4,4(99 оценок)

Ответ:

guna3

16.02.2022

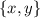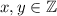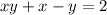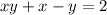Найти все $\displaystyle \{x,y\}$ такие, что $\displaystyle x,y\in\mathbb{Z}$ и $\displaystyle xy+x-y=2$ .

Решим $\displaystyle xy+x-y=2$ для $\displaystyle x$ .
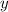Прибавим $\displaystyle y$ к обеим частям уравнения: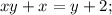
$\displaystyle xy+x=y+2;$
Вынесем $\displaystyle x$ за скобки в левой части уравнения:
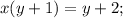
$\displaystyle x(y+1)=y+2;$
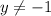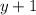Рассмотрим случай, когда $\displaystyle y\neq{-1}$ , и разделим обе части уравнения на $\displaystyle y+1$ :
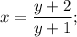
$\displaystyle x=\frac{y+2}{y+1};$
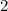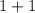Запишем член $\displaystyle 2$ в числителе в правой части уравнения как $\displaystyle 1+1$ :
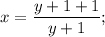
$\displaystyle x=\frac{y+1+1}{y+1};$
Разобём дробь в правой части уравнения на сумму дробей:
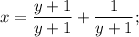
$\displaystyle x=\frac{y+1}{y+1}+\frac{1}{y+1};$
Упростим:
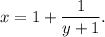
$\displaystyle x=1+\frac{1}{y+1}.$

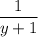Заметим, что $\displaystyle x$ является целым тогда и только тогда, когда член $\displaystyle\frac{1}{y+1}$ в правой части уравнения является целым.

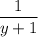Член $\displaystyle\frac{1}{y+1}$ является целым тогда и только тогда, когда знаменатель противоположен или является делителем числителя.

Числитель $\displaystyle 1$ имеет ровно один делитель: $\displaystyle 1$ . Получаем:
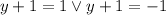$\displaystyle y+1=1 \lor y+1=-1$ .
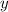Решим для $\displaystyle y$ .
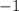Прибавим $\displaystyle -1$ к обеим частям уравнений:
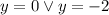$\displaystyle y=0 \lor y=-2$ .

Подставим в исходное уравнение, решённое для $\displaystyle x$ :
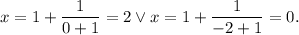
$\displaystyle x=1+\frac{1}{0+1}=2 \lor x=1+\frac{1}{-2+1}=0.$

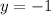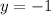Проверим, есть ли решения при исключённом случае $\displaystyle y=-1$ , подставив в исходное уравнение $\displaystyle y=-1$ :
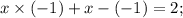
$\displaystyle x\times(-1)+x-(-1)=2;$
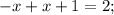
$\displaystyle -x+x+1=2;$
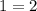$\displaystyle 1=2$ , следовательно, при 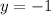$\displaystyle y=-1$ решений нет.

$\displaystyle\boxed{x=0 \land y=-2 \lor x=2 \land y=0}\phantom{.}.$