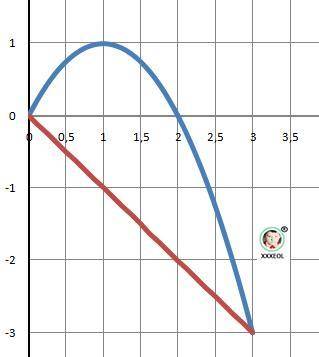
Дано: F(x) = -x² + 2*x , y(x)= -x. Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков: F(x)=y(x).
-x²+3*x=0 - квадратное уравнение
b = 3- верхний предел, a = 0 - нижний предел.
2) Площадь - интеграл разности функций. Прямая ниже параболы.
(F(x) - y(x))dx = -3*x + x² - подинтегральная функция
3) Интегрируем функцию и получаем:
S(x) = -(3/2)*x² + (1/3)*x³
4) Вычисляем на границах интегрирования.
S(b) = S(3) = -13,5 + 9 = -4,5 ÷
S(a) = S(0) = 0
S = S(0)- S(3) = 4,5(ед.²) - площадь - ответ
Рисунок к задаче в приложении.
Написание формул с интегралами здесь сложно. Откорректируйте самостоятельно.
Пошаговое объяснение:
4). Система неравенств:
3х<30; х<30/3; х1<10
5-х≥9; х≤5-9; х2≤-4
х принадлежит (-∞; -4]
5). Система неравенств:
х/2 -х/3<11/6; (3х-2х)/6<11/6; х1<11
7(х-1)≥14; х-1≥14/7; х≥2+1; х2≥3
х принадлежит [3;; 11)
6). Система неравенств:
х/3 -х/4≤7/12
6(х+13)>18
(4х-3х)/12≤7/12
х1≤7
х+13>3
х>3-13
х2>-10
х принадлежит (-10; 7]
7). Система неравенств:
7х-10≤3(х-1)+21
(3х-5)/5>(х-1)/2 -1
7х-10≤3х-3+21
7х-3х≤18+10
4х≤28
х≤28/4
х1≤7
(3х-5)/5>(х-1-2)/2
2(3х-5)>5(х-3)
6х-10>5х-15
6х-5х>10-15
х2>-5
х принадлежит (-5; 7]
8). Система неравенств:
9х+8>4(х-2)-14
(х+9)/4≤3 -(3-х)/6
9х+8>4х-8-14
9х+8>4х-22
4х-9х<8+22
-5х<30
х>30/(-5)
х1>-6
(х+9)/4≤(18-3+х)/6
3(х+9)≤2(15+х)
3х+27≤30+2х
3х-2х≥30-27
х2≥3
х принадлежит [3; +∞)