Пошаговое объяснение:
1)
Дано
Цилиндр
Sкв.=36см² осевое сечение.
Sбок.=?
Решение.
Sкв.=а², где а сторона квадрата.
Найдем сторону квадрата.
а=√Sкв.=√36=6 см
Сторона квадрата является диаметром окружности цилиндра, найдем радиус.
R=d/2=a/2
R=6/2=3
а=h
Sбок.=2πRh
Sбок.=2π*3*6=36π см²
π≈3,14
Sбок.=36*3,14=113,04 см²
ответ: 113,04 см²
3)
Дано
Конус
Сечение равносторонний треугольник
l=12cm сторона треугольника, и образующая
D=l
Sпол.=?
Решение
Одна из сторон треугольника является диаметром окружности конуса. Найдем радиус
R=D/2=12/2=6 cm
Sпол.=πR(l+R)
Sпол.=6π(12+6)
Sпол.=6π*18=108π см²
π≈3,14
Sпол.=339,12 см²
ответ: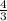
Пошаговое объяснение:
Воспользуемся интегралами для решения данной задачи. Если просто решить уравнения, то получим, что ограниченная область лежит на отрезке x ∈ [0,2]. У параболы и у прямой никаких выколотых точек и других проблем там нет => можем брать определенный интеграл. Определять площадь фигуры будем определять через разность двух определенных интегралов:
Площадь под параболой определим через этот интеграл( пусть будет S1):
S1 =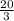
Теперь посчитаем площадь под прямой и назовем ее S2(можно делать и трапецией)
S2 = 8;
Теперь вычтем из S2, S1 и получим площадь фигуры S:
S = S2 -S1 =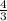
(Если нужно, первообразная параболы будет x^3/3 + 2x, а первообразная прямой x^2 + 2x)